
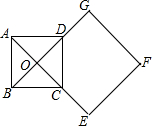
 如图,正方形ABCD的对角线相交于点O,正方形OEFG的一边OG经过点D,且D是OG的中点,OG=$\sqrt{2}$AB,若正方形ABCD固定,将正方形OEFG绕O点逆时针旋转α角,(0°<α<360°)得到正方形OE′F′G′,当α=30或150度时,∠OAG′=90°.
如图,正方形ABCD的对角线相交于点O,正方形OEFG的一边OG经过点D,且D是OG的中点,OG=$\sqrt{2}$AB,若正方形ABCD固定,将正方形OEFG绕O点逆时针旋转α角,(0°<α<360°)得到正方形OE′F′G′,当α=30或150度时,∠OAG′=90°. 分析 根据题意和锐角正弦的概念以及特殊角的三角函数值得到∠AG′O=30°,分两种情况求出α的度数.
解答 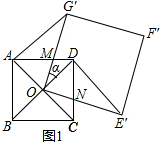 解:当α为锐角时,如图1所示:
解:当α为锐角时,如图1所示:
∵四边形ABCD是正方形,
∴BC=AB,∠ABC=90°,OA=OD=$\frac{1}{2}$AC,
∴AC=$\sqrt{2}$AB,
∵OG=$\sqrt{2}$AB,
∴OG′=OG=AC=2AO,
∵∠OAG′=90°,OA=$\frac{1}{2}$OG′,
∴∠AG′O=30°,
∴∠AOG′=60°,
∴∠DOG′=90°-60°=30°,
即α=30°;
当旋转到如图2所示位置,同理证得∠AG′O=30°,
∴∠AOG′=60°,
∴α=90°+60°=150°,
综上所述:α的度数为30°或150°,
故答案为:30°或150°.
点评 本题考查的是正方形的性质、旋转变换的性质以及锐角三角函数的定义,掌握正方形的四条边相等、四个角相等,旋转变换的性质是解题的关键,注意特殊角的三角函数值的应用.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\sqrt{2}$ | B. | $\sqrt{2}$ | C. | $\frac{1}{\sqrt{2}}$ | D. | -$\frac{1}{\sqrt{2}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
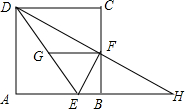 如图,正方形ABCD中,点E在AB上,且BE=$\frac{1}{4}$AB,点F是BC的中点,点G是DE的中点,延长DF,与AB的延长线交于点H.以下四个结论:
如图,正方形ABCD中,点E在AB上,且BE=$\frac{1}{4}$AB,点F是BC的中点,点G是DE的中点,延长DF,与AB的延长线交于点H.以下四个结论:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
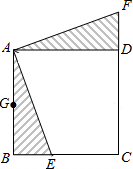 如图,在正方形ABCD中,E是BC上一点,△ABE经过旋转后得到△ADF.
如图,在正方形ABCD中,E是BC上一点,△ABE经过旋转后得到△ADF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com