
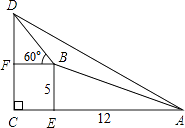
【题目】小明去爬山,在山脚看山顶角度为30°,小明在坡比为5:12的山坡上走1300米,此时小明看山顶的角度为60°,求山高( )
A.600﹣250 ![]() 米
米
B.600 ![]() ﹣250米
﹣250米
C.350+350 ![]() 米
米
D.500 ![]() 米
米
【答案】B
【解析】解:∵BE:AE=5:12,
![]() =13,
=13,
∴BE:AE:AB=5:12:13,
∵AB=1300米,
∴AE=1200米,
BE=500米,
设EC=x米,
∵∠DBF=60°,
∴DF= ![]() x米.
x米.
又∵∠DAC=30°,
∴AC= ![]() CD.
CD.
即:1200+x= ![]() (500+
(500+ ![]() x),
x),
解得x=600﹣250 ![]() .
.
∴DF= ![]() x=600
x=600 ![]() ﹣750,
﹣750,
∴CD=DF+CF=600 ![]() ﹣250(米).
﹣250(米).
答:山高CD为(600 ![]() ﹣250)米.
﹣250)米.
故选:B.
【考点精析】解答此题的关键在于理解关于坡度坡角问题的相关知识,掌握坡面的铅直高度h和水平宽度l的比叫做坡度(坡比).用字母i表示,即i=h/l.把坡面与水平面的夹角记作A(叫做坡角),那么i=h/l=tanA.


 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:
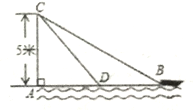
【题目】在杭州西湖风景游船处,如图,在离水面高度为5m的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为13m,此人以0.5m/s的速度收绳.10s后船移动到点D的位置,问船向岸边移动了多少m?(假设绳子是直的,结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中的两点A(m,0),B(2m,0)(m>0),二次函数y=ax2+bx+m的图象与x轴交与A,B两点与y轴交于点C,顶点为点D.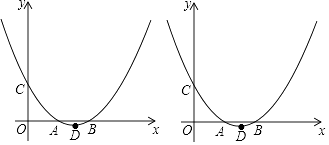
(1)当m=1时,直线BC的解析式为 , 二次函数y=ax2+bx+m的解析式为;
(2)求二次函数y=ax2+bx+m的解析式为(用含m的式子表示);
(3)连接AC、AD、BD,请你探究 ![]() 的值是否与m有关?若有关,求出它与m的关系;若无关,说明理由;
的值是否与m有关?若有关,求出它与m的关系;若无关,说明理由;
(4)当m为正整数时,依次得到点A1 , A2 , …,Am的横坐标分别为1,2,…m;点B1 , B2 , …,Bm 的横坐标分别为2,4,…2m(m≤10);经过点A1 , B1 , 点A2 , B2 , …,点Am , Bm的这组抛物线y=ax2+bx+m分别与y轴交于点C1 , C2 , …,Cm , 由此得到了一组直线B1C1 , B2C2 , …,BmCm , 在点B1 , B2 , …,Bm 中任取一点Bn , 以线段OBn为边向上作正方形OBnEnFn , 若点En在这组直线中的一条直线上,直接写出所有满足条件的点En的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a>b,选择适当的不等号填空:
(1)-![]() ________-
________-![]() ;
;
(2)1-5a__________1-5b;
(3)ax2_________bx2;
(4)a(-c2-1)_________b(-c2-1).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的方程(m-1)x2+(m+1)x+3m-1=0,当m_________时,是一元一次方程;当m_________时,是一元二次方程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线l与⊙O相离,OA⊥l于点A,OA=5.OA与⊙O相交于点P,AB与⊙O相切于点B,BP的延长线交直线l于点C. 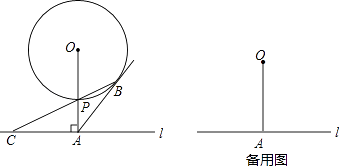
(1)试判断线段AB与AC的数量关系,并说明理由;
(2)若PC=2 ![]() ,求⊙O的半径和线段PB的长;
,求⊙O的半径和线段PB的长;
(3)若在⊙O上存在点Q,使△QAC是以AC为底边的等腰三角形,求⊙O的半径r的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
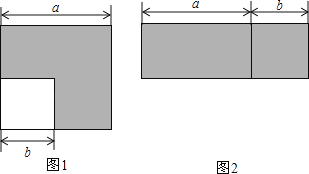
【题目】如图1所示,边长为a的正方形中有一个边长为b的小正方形,如图2所示是由图1中阴影部分拼成的一个正方形.
(1)设图1中阴影部分面积为S1,图2中阴影部分面积为S2.请直接用含a,b的代数式表示S1,S2;
(2)请写出上述过程所揭示的乘法公式;
(3)试利用这个公式计算:(2+1)(22+1)(24+1)(28+1)+1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=BC,CD⊥AB于D点,M,N是AC,BC上的动点,且∠MDN=90°,下列结论:①AM=CN;②四边形MDNC的面积为定值;③AM2+BN2=MN2;④NM平分∠CND.其中正确的是 ( )

A. ①②③ B. ①②④ C. ①③④ D. ①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com