
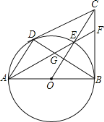
【题目】如图,已知![]() 为
为![]() 的直径,
的直径,![]() 、
、![]() 为的切线,
为的切线,![]() 、
、![]() 为切点,连接
为切点,连接![]() 、
、![]() ,
,![]() 交于点
交于点![]() ,
,![]() 交
交![]() 于
于![]() ,
,![]() 的延长线交
的延长线交![]() 于点
于点![]() ,给出下列结论:①
,给出下列结论:①![]() ;②点
;②点![]() 为
为![]() 的内心;③
的内心;③![]() ;④
;④![]() ,其中正确的是( )
,其中正确的是( )
A. ① B. ①② C. ①②③ D. ①②③④
【答案】C
【解析】
①根据切线长定理,证△COB≌△COD,可得∠DCO=∠BCO.故OC⊥BD.根据圆周角定理即可得出AD⊥BD,由此可证得AD∥OC;
②连接DE、BE;上面已证得![]() =
=![]() ,根据弦切角定理以及圆周角定理相等,易求得DE、BE分别平分∠CDB和∠CBD;根据三角形内心的定义,即可得出结论②正确;
,根据弦切角定理以及圆周角定理相等,易求得DE、BE分别平分∠CDB和∠CBD;根据三角形内心的定义,即可得出结论②正确;
③根据圆周角定理得到,GF⊥BE.又由②知,BE是∠CBD的平分线,根据等腰三角形的“三合一”性质得到EG=EF.故③正确;
④若FE=FC,则∠OCB=∠CEF=∠OEA=∠OAE,在Rt△OBC中,BD⊥OC,易得∠DBA=∠OCB(因为OC⊥BD),即∠DBA=∠EAB;因此![]() =
=![]() ,而这个条件并不一定成立.故④不正确.
,而这个条件并不一定成立.故④不正确.
①连接OD,DE,EB,CD,与BC是O的切线,易证△CDO≌△CBO,则∠DCO=∠BCO.故OC⊥BD.∵AB是直径,∴AD⊥BD,∴AD∥OC,故①正确;②∵CD是O的切线,∴∠CDE=12∠DOE,而∠BDE=12∠BOE,∴∠CDE=∠BDE,即DE是∠CDB的角平分线,同理可证得BE是∠CBD的平分线,因此E为△CBD的内心,故②正确;③如图,∵AB是直径,∴∠AEB=90,即GF⊥BE.又由②知,BE是∠CBD的平分线,∴BE是等腰△GBF的边GF上的中垂线,则EG=EF.故③正确;④若FC=FE,则应有∠OCB=∠CEF,应有∠CEF=∠AEO=∠EAB=∠DBA=∠DEA,∴![]() =
=![]() ,而
,而![]() 和
和![]() 不一定相等,故④不正确.故选C.
不一定相等,故④不正确.故选C.


 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,已知AB=AC,D是AC上的一点,CD=9,BC=15,BD=12.

(1)证明:△BCD是直角三角形.
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读)
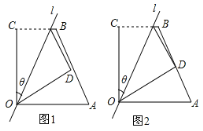
如图1,四边形OABC中,OA=a,OC=8,BC=6,∠AOC=∠BCO=90°,经过点O的直线l将四边形分成两部分,直线l与OC所成的角设为θ,将四边形OABC的直角∠OCB沿直线l折叠,点C落在点D处,我们把这个操作过程记为FZ[θ,a].
(理解)
若点D与点A重合,则这个操作过程为FZ[45°,8];
(尝试)
(1)若点D与OA的中点重合,则这个操作过程为FZ[____,____];
(2)若点D恰为AB的中点(如图2),求θ的值;
(应用)
经过FZ[45°,a]操作,点B落在点E处,若点E在四边形OABC的边AB上,直线l与AB相交于点F,试画出图形并解决下列问题:
①求出a的值;
②若P为边OA上一动点,连接PE、PF,请直接写出PE+PF的最小值.
(备注:等腰直角三角形的三边关系满足![]() 或
或![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)阅读理解:
如图①,在△ABC中,若AB=10,AC=6,求BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使DE=AD,再连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD),把AB、AC,2AD集中在△ABE中,利用三角形三边的关系即可判断.
中线AD的取值范围是 ;
(2)问题解决:
如图②,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证:BE+CF>EF;
(3)问题拓展:
如图③,在四边形ABCD中,∠B+∠D=180°,CB=CD,∠BCD=140°,以为顶点作一个70°角,角的两边分别交AB,AD于E、F两点,连接EF,探索线段BE,DF,EF之间的数量关系,并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】天猫网的新时代书店准备购进甲、乙两种图书,已知甲种图书进价比乙种图书贵4元,用3000元购进甲种图书的数量与用2400元购进乙种图书的数量相同.
(1)甲、乙两种图书的单价分别为多少元?
(2)若甲种图书每本售价30元,乙种图书每本售价25元,书店欲同时购进两种图书共100本,请写出所获利润y(单位:元)关于甲种图书x(单位:本)的函数解析式;
(3)在(2)的条件下,若书店计划用不超过1800元购进两种图书,且甲种图书至少购进40本,并将所购图书全部销售,共有多少种购进方案?哪一种方案利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小华的爸爸要用一块矩形铁皮加工出一个底面半径为![]() ,高为
,高为![]() 的锥形漏斗,要求只能有一条接缝(接缝忽略不计)
的锥形漏斗,要求只能有一条接缝(接缝忽略不计)
![]() 你能求出这个锥形漏斗的侧面展开图的圆心角吗?
你能求出这个锥形漏斗的侧面展开图的圆心角吗?
![]() 如图,有两种设计方案,请你计算一下,哪种方案所用的矩形铁皮面积较少?
如图,有两种设计方案,请你计算一下,哪种方案所用的矩形铁皮面积较少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点![]() 若点D为BC边的中点,点M为线段EF上一动点,则
若点D为BC边的中点,点M为线段EF上一动点,则![]() 周长的最小值为
周长的最小值为![]()
![]()

A. 6 B. 8 C. 10 D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A的坐标为(﹣![]() ,0),点B的坐标为(0,3).
,0),点B的坐标为(0,3).
(1)求过A,B两点直线的函数表达式;
(2)过B点作直线BP与x轴交于点P,且使OP=2OA,求△ABP的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知等腰直角![]() 中,BD为斜边上的中线,E为DC上的一点,且
中,BD为斜边上的中线,E为DC上的一点,且![]() 于G,AG交BD于F.
于G,AG交BD于F.
(1)求证:AF=BE.
(2)如图②,当点E在DC的延长线上,其它条件不变,①的结论还能成立吗?若不能,请说明理由;若能,请予以证明。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com