
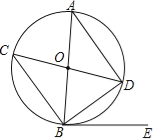
【题目】如图,在⊙O中,AB,CD是直径,BE是切线,B为切点,连接AD,BC,BD.
(1)求证:△ABD≌△CDB;
(2)若∠DBE=37°,求∠ADC的度数.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】数学课上学习了圆周角的概念和性质:“顶点在圆上,两边与圆相交”,“同弧所对的圆周角相等”,小明在课后继续对圆外角和圆内角进行了探究.
下面是他的探究过程,请补充完整:
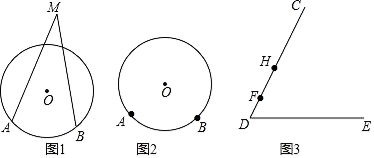
定义概念:顶点在圆外,两边与圆相交的角叫做圆外角,顶点在圆内,两边与圆相交的角叫做圆内角.如图1,∠M为![]() 所对的一个圆外角.
所对的一个圆外角.
(1)请在图2中画出![]() 所对的一个圆内角;
所对的一个圆内角;
提出猜想
(2)通过多次画图、测量,获得了两个猜想:一条弧所对的圆外角______这条弧所对的圆周角;一条弧所对的圆内角______这条弧所对的圆周角;(填“大于”、“等于”或“小于”)
推理证明:
(3)利用图1或图2,在以上两个猜想中任选一个进行证明;
问题解决
经过证明后,上述两个猜想都是正确的,继续探究发现,还可以解决下面的问题.
(4)如图3,F,H是∠CDE的边DC上两点,在边DE上找一点P使得∠FPH最大.请简述如何确定点P的位置.(写出思路即可,不要求写出作法和画图)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于反比例函数y=![]() (k≠0),下列说法不正确的是( )
(k≠0),下列说法不正确的是( )
A. 它的图象分布在第一、三象限 B. 点(k,k)在它的图象上
C. 它的图象关于原点对称 D. 在每个象限内y随x的增大而增大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC内接于⊙O,过点A作直线EF.
(1)如图①,AB是直径,要使EF是⊙O的切线,还须添加一个条件是(只需写出三种情况).
(ī) (īī) (īīī)
(2)如图(2),若AB为非直径的弦,∠CAE=∠B,则EF是⊙O的切线吗?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C都在抛物线y=ax2﹣2amx+am2+2m﹣5(其中﹣![]() <a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
<a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
(1)填空:抛物线的顶点坐标为 (用含m的代数式表示);
(2)求△ABC的面积(用含a的代数式表示);
(3)若△ABC的面积为2,当2m﹣5≤x≤2m﹣2时,y的最大值为2,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分10分)
如图,台风中心位于点P,并沿东北方向PQ移动,已知台风移动的速度为30千米/时,受影响区域的半径为200千米,B市位于点P的北偏东75°方向上,距离点P 320千米处.

(1) 说明本次台风会影响B市;
(2)求这次台风影响B市的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
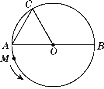
【题目】如图,在⊙O中,AB为⊙O的直径,AC是弦,OC=4,∠OAC=60°.
(1)求∠AOC的度数;
(2)如图,一动点M从A点出发,在⊙O上按逆时针方向运动,当S△MAO=S△CAO时,求动点M所经过的弧长.
查看答案和解析>>
科目:初中数学 来源: 题型:
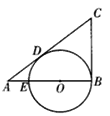
【题目】如图,在△ABC中,已知∠ABC=90o,在AB上取一点E,以BE为直径的⊙O恰与AC相切于点D,若AE=2cm,AD=4cm.
(1)求⊙O的直径BE的长;
(2)计算△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com