
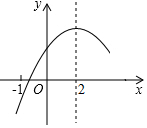 ¶ž“ĪŗÆŹży=ax2+bx+c£Øa”Ł0£©µÄ²æ·ÖĶ¼ĻóČēĶ¼¢ŪĖłŹ¾£¬Ķ¼Ļó¹żµć£Ø-1£¬0£©£¬¶Ō³ĘÖįĪŖÖ±Ļßx=2£¬ŌņĻĀ ĮŠ½įĀŪÖŠÕżČ·µÄøöŹżÓŠ£Ø””””£©
¶ž“ĪŗÆŹży=ax2+bx+c£Øa”Ł0£©µÄ²æ·ÖĶ¼ĻóČēĶ¼¢ŪĖłŹ¾£¬Ķ¼Ļó¹żµć£Ø-1£¬0£©£¬¶Ō³ĘÖįĪŖÖ±Ļßx=2£¬ŌņĻĀ ĮŠ½įĀŪÖŠÕżČ·µÄøöŹżÓŠ£Ø””””£©| A£® | 1øö | B£® | 2øö | C£® | 3øö | D£® | 4øö |
·ÖĪö ÓÉÅ×ĪļĻ߶Ō³ĘÖįæÉÅŠ¶Ļ¢Ł£»ÓÉÅ×ĪļĻߵĶŌ³ĘŠŌÖŖx=3Ź±£¬y£¾0£¬æÉÅŠ¶Ļ¢Ś£»øł¾Ż¶ž“ĪŗÆŹżµÄŌö¼õŠŌÖŖÅ×ĪļĻßÉĻĄė¶Ō³ĘÖįĖ®Ę½¾ąĄėŌ½Š”£¬ŗÆŹżÖµŌ½“󣬾Ż“ĖæÉÅŠ¶Ļ¢Ū£»·½³Ģa£Øx+1£©£Øx-5£©=-3µÄĮ½øł¼“ĪŖÅ×ĪļĻßy=a£Øx+1£©£Øx-5£©ÓėÖ±Ļßy=-3½»µćµÄŗį×ų±ź£¬¾Ż“ĖæÉÅŠ¶Ļ¢Ü£®
½ā“š ½ā£ŗÓÉÅ×ĪļĻߵĶŌ³ĘÖįĪŖx=2æɵĆ-$\frac{b}{2a}$=2£¬¼“4a+b=0£¬¹Ź¢ŁÕżČ·£»
ÓÉÅ×ĪļĻߵĶŌ³ĘŠŌÖŖx=0ŗĶx=4Ź±£¬y£¾0£¬
Ōņx=3Ź±£¬y=9a+3b+c£¾0£¬¹Ź¢Ś“ķĪó£»
”ßÅ×ĪļĻßµÄæŖæŚĻņĻĀ£¬ĒŅ¶Ō³ĘÖįĪŖx=2£¬
”ąÅ×ĪļĻßÉĻĄė¶Ō³ĘÖįĖ®Ę½¾ąĄėŌ½Š”£¬ŗÆŹżÖµŌ½“ó£¬
”ßµćAµ½x=2µÄĖ®Ę½¾ąĄėĪŖ5£¬µćBµ½¶Ō³ĘÖįµÄĖ®Ę½¾ąĄėĪŖ2.5£¬µćCµ½¶Ō³ĘÖįµÄĖ®Ę½¾ąĄėĪŖ3£¬
”ąy1£¼y3£¼y2£¬¹Ź¢ŪÕżČ·£»
Įīy=a£Øx+1£©£Øx-5£©£¬
ŌņÅ×ĪļĻßy=a£Øx+1£©£Øx-5£©Óėy=ax2+bx+cŠĪדĻąĶ¬”¢æŖæŚ·½ĻņĻąĶ¬£¬ĒŅÓėxÖįµÄ½»µćĪŖ£Ø-1£¬0£©”¢£Ø3£¬0£©£¬
ŗÆŹżĶ¼ĻóČēĶ¼ĖłŹ¾£¬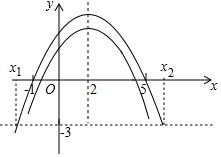
ÓÉŗÆŹżĶ¼ĻóæÉÖŖ·½³Ģa£Øx+1£©£Øx-5£©=-3µÄĮ½øł¼“ĪŖÅ×ĪļĻßy=a£Øx+1£©£Øx-5£©ÓėÖ±Ļßy=-3½»µćµÄŗį×ų±ź£¬
”ąx1£¼-1£¼5£¼x2£¬¹Ź¢ÜÕżČ·£»
¹ŹŃ”£ŗC£®
µćĘĄ ±¾ĢāÖ÷ŅŖæ¼²éÅ×ĪļĻßÓėxÖįµÄ½»µćĪŹĢā¼°¶ž“ĪŗÆŹżĶ¼ĻóÓėĻµŹżµÄ¹ŲĻµ£¬¶ž“ĪŗÆŹży=ax2+bx+cĻµŹż·ūŗÅÓÉÅ×ĪļĻßæŖæŚ·½Ļņ”¢¶Ō³ĘÖį”¢Å×ĪļĻßÓėyÖįµÄ½»µć”¢Å×ĪļĻßÓėxÖį½»µćµÄøöŹżČ·¶Ø£®


 ĆūŠ£æĪĢĆĻµĮŠ“š°ø
ĆūŠ£æĪĢĆĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
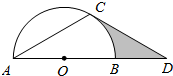 ČēĶ¼£¬µćDŌŚ”ŃOµÄÖ±¾¶ABµÄŃÓ³¤ĻßÉĻ£¬µćCŌŚ”ŃOÉĻ£¬AC=CD£¬”ĻACD=120”ć£®
ČēĶ¼£¬µćDŌŚ”ŃOµÄÖ±¾¶ABµÄŃÓ³¤ĻßÉĻ£¬µćCŌŚ”ŃOÉĻ£¬AC=CD£¬”ĻACD=120”ć£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | 5.17”Į103 | B£® | 51.7”Į104 | C£® | 5.17”Į105 | D£® | 5.17”Į106 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | 3.5”Į1010 | B£® | 3.5”Į109 | C£® | 3.5”Į108 | D£® | 3.5”Į107 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
 ČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬Ņ»¶Æµć“ÓŌµćO³ö·¢£¬ŃŲ׿żĶ·ĖłŹ¾·½Ļņ£¬Ćæ“ĪŅʶÆ1øöµ„Ī»£¬ŅĄ“ĪµĆµ½µćP1£Ø0£¬1£©£¬P2£Ø1£¬1£©£¬P3£Ø1£¬0£©£¬P4£Ø1£¬-1£©£¬P5£Ø2£¬-1£©£¬P6£Ø2£¬0£©£¬”£¬ŌņµćP90µÄ×ų±źŹĒ£Ø30£¬0£©£®
ČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬Ņ»¶Æµć“ÓŌµćO³ö·¢£¬ŃŲ׿żĶ·ĖłŹ¾·½Ļņ£¬Ćæ“ĪŅʶÆ1øöµ„Ī»£¬ŅĄ“ĪµĆµ½µćP1£Ø0£¬1£©£¬P2£Ø1£¬1£©£¬P3£Ø1£¬0£©£¬P4£Ø1£¬-1£©£¬P5£Ø2£¬-1£©£¬P6£Ø2£¬0£©£¬”£¬ŌņµćP90µÄ×ų±źŹĒ£Ø30£¬0£©£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | 1800”ć | B£® | 1620”ć | C£® | 1440”ć | D£® | 1260”ć |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | £Ø-$\frac{1}{2}$£¬1£© | B£® | £Ø2£¬-1£© | C£® | £Ø-1£¬2£© | D£® | £Ø1£¬$\frac{1}{2}$£© |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
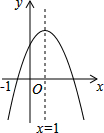 ŅŃÖŖ¶ž“ĪŗÆŹżµÄĶ¼ĻóČēĶ¼£¬ŌņĻĀĮŠ½įĀŪÖŠÕżČ·µÄÓŠ£Ø””””£©
ŅŃÖŖ¶ž“ĪŗÆŹżµÄĶ¼ĻóČēĶ¼£¬ŌņĻĀĮŠ½įĀŪÖŠÕżČ·µÄÓŠ£Ø””””£©| A£® | 5øö | B£® | 4øö | C£® | 3øö | D£® | 2øö |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | 2 | B£® | 3 | C£® | 4 | D£® | 5 |
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com