Question

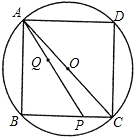
如图，△ABC内接于⊙O，∠B=90°，AB=BC，D是⊙O上与点B关于圆心O成中心对称的点，P是BC边上一点，连接AD、DC、AP．已知AB=8，CP=2，Q是线段AP上一动点，连接BQ并延长交四边形ABCD的一边于点R，且满足AP=BR，则

BQ

QR

的值为

 

．

Answer 1

分析：先证明四边形ABCD是正方形，得出AD∥BC．根据题意，可知点R所在的位置可能有两种情况：①点R在线段AD上；②点R在线段CD上．针对每一种情况，分别求出BQ：QR的值．

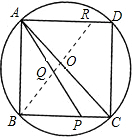解答：解：∵△ABC内接于⊙O，∠B=90°，AB=BC，D是⊙O上与点B关于圆心O成中心对称的点，
∴四边形ABCD是正方形．
∴AD∥BC，
当AP=BR时，分两种情况：
①点R在线段AD上，
∵AD∥BC，
∴∠ARB=∠PBR，∠RAQ=∠APB，
在△AQR与△PQB中，
∵

∠RAQ=∠QPB AR=BP ∠ARB=∠RBP

，
∴△AQR≌△PQB，
∴BQ=QR
∴BQ：QR=1；
②点R在线段CD上，此时△ABP≌△BCR，
∴∠BAP=∠CBR．
∵∠CBR+∠ABR=90°，
∴∠BAP+∠ABR=90°，
∴BQ是直角△ABP斜边上的高，
∴BQ=

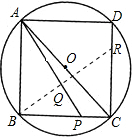
AB•BP

AP

=

8×6

10

=4.8，
∴QR=BR-BQ=10-4.8=5.2，
∴BQ：QR=4.8：5.2=

12

13

．
故答案为：1或

12

13

．

点评：本题综合考查了平行线的判定，及正方形的判定，及全等的判定及性质．