
【题目】已知如图,![]() 是
是![]() 的直径,点
的直径,点![]() 在
在![]() 上,且
上,且![]() ,点
,点![]() 是
是![]() 外一点,
外一点,![]() 与
与![]() 相切于点
相切于点![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .
.
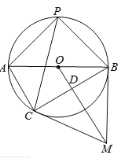
(1)求证:![]() ;
;
(2)求证:![]() 是
是![]() 的切线;
的切线;
(3)若![]() ,
,![]() ,连接
,连接![]() ,求
,求![]() 的长;
的长;
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)利用平行证出△BOD∽△BAC,然后列出比例式即可求出结论;
(2)连接OC,利用SAS证出△BOM≌△COM,从而证出∠OBM=∠OMB,然后根据切线的性质即可证出结论;
(3)过点A作AE⊥PC于E,根据相似三角形的判定定理证出△DOC∽△DCM,列出比例式即可求出CD,根据勾股定理求出OC,从而求出AB,然后利用锐角三角函数求出PA、AE和CE,从而求出结论.
解:(1)∵![]() ,AB=2OB
,AB=2OB
∴△BOD∽△BAC
∴![]()
∴![]() ;
;
(2)连接OC
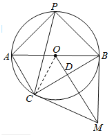
∵![]()
∴∠BOM=∠BAC
∵![]()
∴∠BOC=2∠BAC=2∠BOM
∴∠BOM=∠COM
在△BOM和△COM中
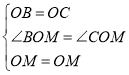
∴△BOM≌△COM
∴∠OBM=∠OMB
∵![]() 与
与![]() 相切于点
相切于点![]() ,
,
∴∠OBM=90°,
∴∠OMB=90°
∴![]() 是
是![]() 的切线;
的切线;
(3)过点A作AE⊥PC于E
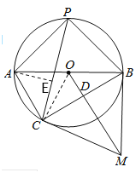
∵AB为直径
∴∠ACB=∠APB=90°
∵![]() ,
,
∴∠CDM=∠ACB =90°,∠ODC=90°
∵∠OCM=90°,
∴∠DOC+∠OCD=90°,∠DCM+∠OCD=90°
∴∠DOC=∠DCM
∴△DOC∽△DCM
∴![]()
即![]()
解得:CD=12
根据勾股定理可得OC=![]()
∴AB=2OC=30
由(1)知AC=2OD=18
∵![]()
∴△PAB为等腰直角三角形,
∴∠PAB=∠PBA=45°,
∴∠ACP=∠PBA=45°,PA=AB·sin∠PBA=![]()
∴△ACE为等腰直角三角形
∴∠ECA=45°
∴CE=AE=AC·sin∠ECA=![]()
根据勾股定理PE=![]()
∴PC=PE+CE=![]()


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:
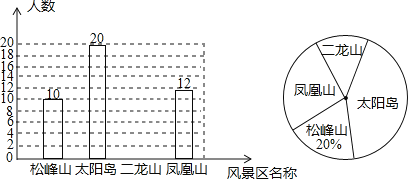
【题目】随着社会经济的发展和城市周边交通状况的改善,旅游已成为人们的一种生活时尚,洪祥中学开展以“我最喜欢的风景区”为主题的调查活动,围绕“在松峰山、太阳岛、二龙山和凤凰山四个风景区中,你最喜欢哪一个?(必选且只选一个)”的问题,在全校范围内随机抽取了部分学生进行问卷调查,将调查结果整理后绘制成如图所示的不完整的统计图,请你根据图中提供的信息回答下列问题:
(1)本次调查共抽取了多少名学生?
(2)通过计算补全条形统计图;
(3)若洪祥中学共有1350名学生,请你估计最喜欢太阳岛风景区的学生有多少名.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某足球运动员站在点O处练习射门,将足球从离地面0.5m的A处正对球门踢出(点A在y轴上),足球的飞行高度y(单位:m)与飞行时间t(单位:s)之间满足函数关系y=at2+5t+c,已知足球飞行0.8s时,离地面的高度为3.5m.
(1)足球飞行的时间是多少时,足球离地面最高?最大高度是多少?
(2)若足球飞行的水平距离x(单位:m)与飞行时间t(单位:s)之间具有函数关系x=10t,已知球门的高度为2.44m,如果该运动员正对球门射门时,离球门的水平距离为28m,他能否将球直接射入球门?

查看答案和解析>>
科目:初中数学 来源: 题型:
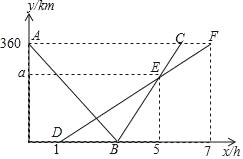
【题目】快、慢两车分别从相距360km的佳市、哈市两地出发,匀速行驶,先相向而行,慢车在快车出发1h后出发,到达佳市后停止行驶,快车到达哈市后,立即按原路原速返回佳市(快车调头的时间忽略不计),快、慢两车距哈市的路程y1(单位:km),y2(单位:km)与快车出发时间x(单位:h)之间的函数图象如图所示,请结合图象信息解答下列问题:
(1)直接写出慢车的行驶速度和a的值;
(2)快车与慢车第一次相遇时,距离佳市的路程是多少千米?
(3)快车出发多少小时后两车相距为100km?请直接写出答案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() (x>0)的图象交于A(2,﹣1)、B(
(x>0)的图象交于A(2,﹣1)、B(![]() ,n)两点.直线y=2与y轴交于点C.
,n)两点.直线y=2与y轴交于点C.
1)求一次函数与反比例函数的解析式;
2)求△ABC的面积;
3)直接写出不等式kx+b>![]() 在如图所示范围内的解集.
在如图所示范围内的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
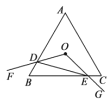
【题目】如图,等边三角形![]() 的边长为4,点
的边长为4,点![]() 是△
是△![]() 的中心,
的中心,![]() .绕点
.绕点![]() 旋转
旋转![]() ,分别交线段
,分别交线段![]() 于
于![]() 两点,连接
两点,连接![]() ,给出下列四个结论:①
,给出下列四个结论:①![]() ;②
;②![]() ;③四边形
;③四边形![]() 的面积始终等于
的面积始终等于![]() ;④△
;④△![]() 周长的最小值为6,上述结论中正确的个数是( )
周长的最小值为6,上述结论中正确的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装公司试销一种成本为每件50元的![]() 恤衫.试销中发现,当销售单价是60元时,售出400件;销售单价每降低1元,多售出10件.设试销中销售单价
恤衫.试销中发现,当销售单价是60元时,售出400件;销售单价每降低1元,多售出10件.设试销中销售单价![]() (元)时的销售量为
(元)时的销售量为![]() (件).
(件).
(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)设该公司获得的总利润为![]() 元,求
元,求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)若要销量不低于200件,且获利至少5250元,则售价应在何范围内?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形纸片ABCD,AB=7,BC=4,在矩形边上有一点P,且DP=3.将矩形纸片折叠,使点B与点P重合,折痕所在直线交矩形两边于点E、F,则EF=__________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
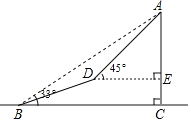
【题目】如图,一座山的一段斜坡BD的长度为600米,且这段斜坡的坡度i=1:3(沿斜坡从B到D时,其升高的高度与水平前进的距离之比).已知在地面B处测得山顶A的仰角为30°,在斜坡D处测得山顶A的仰角为45°.求山顶A到地面BC的高度AC是多少米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com