
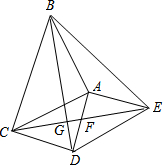
 如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,四边形ACDE是平行四边形,连接CE交AD于点F,连接BD交CE于点G,连接BE;下列结论中:①CE=BD;②∠ADB=∠AEB;③△ADC是等腰直角三角形;④CD•AE=EF•CG;一定正确的结论有( )
如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,四边形ACDE是平行四边形,连接CE交AD于点F,连接BD交CE于点G,连接BE;下列结论中:①CE=BD;②∠ADB=∠AEB;③△ADC是等腰直角三角形;④CD•AE=EF•CG;一定正确的结论有( )| A、1个 | B、2个 | C、3个 | D、4个 |
 解:①∵∠BAC=∠DAE=90°,
解:①∵∠BAC=∠DAE=90°,| CD |
| EF |
| CG |
| AE |


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:
| A、了解宁德市空气质量情况 |
| B、了解闽江流域的水污染情况 |
| C、了解宁德市居民的环保意识 |
| D、了解全班同学每周体育锻炼的时间 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 4 |
| 1 |
| n |
| 180° |
| n |
查看答案和解析>>
科目:初中数学 来源: 题型:
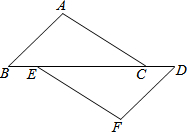 如图,已知点B,E,C,D在同一直线上,AB=FD,∠B=∠D,请你添加一个条件,使AC=FE,并给出证明(不再添加其它线段,不再标注或使用其他字母).你添加的条件是:
如图,已知点B,E,C,D在同一直线上,AB=FD,∠B=∠D,请你添加一个条件,使AC=FE,并给出证明(不再添加其它线段,不再标注或使用其他字母).你添加的条件是:查看答案和解析>>
科目:初中数学 来源: 题型:
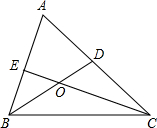 如图,△ABC的两条角平分线BD,CE交于点O
如图,△ABC的两条角平分线BD,CE交于点O查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com