
 如图,在正方形网格上有一个△ABC,如果用(2,1)表示方格纸上A点的位置,(1,2)表示B点的位置,C点的顶点也在网格点上.
如图,在正方形网格上有一个△ABC,如果用(2,1)表示方格纸上A点的位置,(1,2)表示B点的位置,C点的顶点也在网格点上.分析 (1)先利用点A、点B的坐标画出直角坐标系,然后利用网格特点和中心对称的对应画出点A、B、C的对应点A′、B′、C′,从而得到△A′B′C′;
(2)利用点的坐标的表示方法写出A′、B′、C′三点的坐标;
(3)利用一个矩形的面积分别减去三个三角形的面积计算△A′′BC′的面积.
解答 解:(1)如图,△A′B′C′为所作;
(2)A′(4,1),B′(5,0),C′(3,-2);
(3)△A′′BC′的面积=2×3-$\frac{1}{2}$×1×1-$\frac{1}{2}$×2×2-$\frac{1}{2}$×1×3=2.
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:选择题
| A. | (a-b)2=a2-b2 | B. | (a+2b)2=a2+2ab+b2 | C. | (a+b)2=a2+b2 | D. | (-a+b)2=a2-2ab+b2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
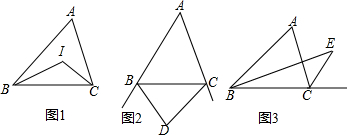
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
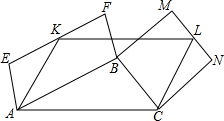 在△ABC的边AC上做平行四边形AKLC,使它与△ABC位于AC的同侧,再以AB和BC为底作平行四边形AEFB和BMNC,使它们与△ABC分别位于AB和BC的两侧,并使EF经过K,MN经过L,猜想平行四边形AKLC的面积与平行四边形AEFB和BMNC的面积的关系,并说明理由.
在△ABC的边AC上做平行四边形AKLC,使它与△ABC位于AC的同侧,再以AB和BC为底作平行四边形AEFB和BMNC,使它们与△ABC分别位于AB和BC的两侧,并使EF经过K,MN经过L,猜想平行四边形AKLC的面积与平行四边形AEFB和BMNC的面积的关系,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,正方形ABCD的面积为36cm2,点E在BC上,点G在AB的延长线上,四边形EFGB是正方形,以点B为圆心,BC的长为半径画$\widehat{AC}$,连接AF,CF,则图中阴影部分的面积为9πcm2.
如图,正方形ABCD的面积为36cm2,点E在BC上,点G在AB的延长线上,四边形EFGB是正方形,以点B为圆心,BC的长为半径画$\widehat{AC}$,连接AF,CF,则图中阴影部分的面积为9πcm2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (x+y)(x2-y2) | B. | x2(x+y)-y2(x+y) | C. | (x+y)(x-y)2 | D. | (x+y)2(x-y) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 去括号 | B. | 去分母 | C. | 移项合并(x-1)项 | D. | 以上方法都可以 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com