
【题目】已知点E在△ABC内,∠ABC=∠EBD=α,∠ACB=∠EDB=60°,∠AEB=150°,∠BEC=90°. 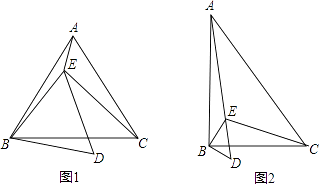
(1)当α=60°时(如图1), ①判断△ABC的形状,并说明理由;
②求证:BD= ![]() AE;
AE;
(2)当α=90°时(如图2),求 ![]() 的值.
的值.
【答案】
(1)解:①判断:△ABC是等边三角形.
理由:∵∠ABC=∠ACB=60°
∴∠BAC=180°﹣∠ABC﹣∠ACB=60°=∠ABC=∠ACB
∴△ABC是等边三角形
②证明:同理△EBD也是等边三角形
连接DC,
则AB=BC,BE=BD,∠ABE=60°﹣∠EBC=∠CBD
∴△ABE≌△CBD
∴AE=CD,∠AEB=∠CDB=150°
∴∠EDC=150°﹣∠BDE=90°∠CED=∠BEC﹣∠BED=90°﹣60°=30°
在Rt△EDC中 ![]() ,
,
∴ ![]()

(2)解:连接DC,
∵∠ABC=∠EBD=90°,∠ACB=∠EDB=60°
∴△ABC∽△EBD
∴ ![]()
又∵∠ABE=90°﹣∠EBC=∠CBD
∴△ABE∽△CBD,∠AEB=∠CDB=150°, ![]()
∴∠EDC=150°﹣∠BDE=90°∠CED=∠BEC﹣∠BED=90°﹣(90°﹣∠BDE)=60°
设BD=x在Rt△EBD中DE=2x,BE= ![]()
在Rt△EDC中CD= ![]()
∴ ![]() ,即
,即 ![]()

【解析】①由三角形ABC中有两个60°而求得它为等边三角形;②由△EBD也是等边三角形,连接DC,证得△ABE≌△CBD,在直角三角形中很容易证得结论.(2)连接DC,证得△ABC∽△EBD,设BD=x在Rt△EBD中DE=2x由相似比即得到比值.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:
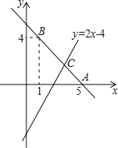
【题目】已知直线y=kx+b经过点A(5,0),B(1,4).
(1)求直线AB的解析式;
(2)若直线y=2x﹣4与直线AB相交于点C,求点C的坐标;
(3)根据图象,写出关于x的不等式2x﹣4>kx+b的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C为⊙O上一点,弦AD平分∠BAC,交BC于点E,AB=6,AD=5,则AE的长为( ) 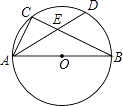
A.2.5
B.2.8
C.3
D.3.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知A点从(1,0)点出发,以每秒1个单位长的速度沿着x轴的正方向运动,经过t秒后,以O、A为顶点作菱形OABC,使B、C点都在第一象限内,且∠AOC=60°,又以P(0,4)为圆心,PC为半径的圆恰好与OA所在的直线相切,则t= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC在直角坐标系中。

(1)请写出△ABC各点的坐标;
(2)求出△ABC的面积S△ABC;
(3)若把△ABC向上平移2个单位,再向右平移2个单位得△A1B1C1,在图中画出△A1B1C1,并写出△A1B1C1的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲、乙分别是4等分、3等分的两个圆转盘,指针固定,转盘转动停止后,指针指向某一数字. 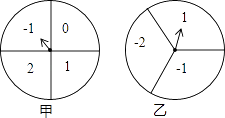
(1)直接写出转动甲盘停止后指针指向数字“1”的概率;
(2)小华和小明利用这两个转盘做游戏,两人分别同时转动甲、乙两个转盘,停止后,指针各指向一个数字,若两数字之积为非负数则小华胜;否则,小明胜.你认为这个游戏公平吗?请你利用列举法说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题
情景:

试根据图中的信息,解答下列问题:
(1)购买6根跳绳需___________元,购买12根跳绳需_____________元.
(2)小红比小明多买2根,付款时小红反而比小明少5元,你认为有这种可能吗?若有,请求出小红购买跳绳的根数;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l上摆放着两块大小相同的直角三角形△ABC和△ECD,∠ACB=∠DCE=90°,且BC=CE=3,AC=CD=4,将△ECD绕点C逆时针旋转到△E1CD1位置,且D1E1∥l ,则B、E1两点之间的距离为___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图,有下列5个结论:
①abc<0;②3a+c>0;③4a+2b+c>0;④2a+b=0;⑤b2>4ac
其中正确的结论的有( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com