Question

已知⊙O₁和⊙O₂外切于A（如图1），BC是它们的一条外公切线，B、C分别为切点，连接AB、AC，
（1）求证：AB⊥AC；
（2）将两圆外公切线BC变为⊙O₁的切线，且为⊙O₂的割线BCD（如图2），其它条件不变，猜想∠BAC+∠BAD的大小，并加以证明；
（3）将两圆外切变为两圆相交于A、D（如图3），其它条件不变，猜想：∠BAC+∠BDC的大小？并加以证明．

Answer 1

（1）

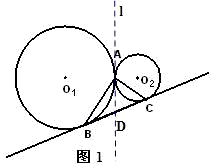
证明：过A作两圆的内公切线l，交BC于D，则由切线的性质知DB=DA=DC，
则三角形ABC为直角三角形．即AB⊥AC；（3分）
（2）

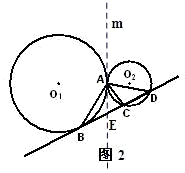
猜想：∠BAC+∠BAD=180°（4分）
证明：过点A作两圆的内公切线m，交BC于E，由切线的性质得，
∠BAE=∠ABC，∠EAC=∠ADC
∴∠BAC=∠BAE+∠EAC=∠ABC+∠ADC（7分），
∴∠BAC+∠BAD=∠ABC+∠ADC+∠BAD=180°；（8分）
（3）

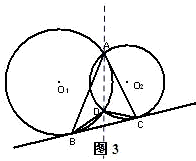
猜想：∠BAC+∠BDC=180°（9分），
证明：连接AD，由于BC是它们的一条外公切线，由切线的性质得，
则∠BAC=∠BAD+∠DAC=∠DBC+∠DCB（12分），
∴∠BAC+∠BDC=∠DBC+∠DCB+∠BDC=180°．（13分）．
分析：（1）首先过A作两圆的内公切线l，交BC于D．根据切线的性质，证得△ABC为直角三角形．进而得到AB⊥AC．
（2）首先过点A作两圆的内公切线m，交BC于E，利用切线的性质与三角形的内角和定理，可证得猜想结论．
（3）连接AD，由于BC是它们的一条外公切线，利用切线的性质与三角形的内角和定理，即可证得猜想结论．
点评：本题考查圆切线的性质、三角形的内角和定理．解决本题的关键是巧妙添加辅助线，仔细分析本题，三个小题添加辅助线具有共性．