
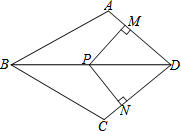
 如图,在四边形ABCD中,DA=DC,P为对角线BD上一点,过点P作PM⊥AD,PN⊥CD,且PM=PN,
如图,在四边形ABCD中,DA=DC,P为对角线BD上一点,过点P作PM⊥AD,PN⊥CD,且PM=PN,分析 (1)根据到角两边距离相等的点在角的平分线上可得DB平分∠ADC,然后再证明△ABD≌△CBD可得AB=BC;
(2)首先根据三个角是直角的四边形是矩形可得四边形PMDN是矩形,再根据邻边相等的矩形是正方形可得结论.
解答 证明:(1)∵PM⊥AD,PN⊥CD,且PM=PN,
∴DB平分∠ADC,
∴∠ADB=∠CDB,
在△ABD和△CBD中,
$\left\{\begin{array}{l}{AD=DC}\\{∠ADB=∠CDB}\\{BD=BD}\end{array}\right.$,
∴△ABD≌△CBD(SAS),
∴AB=BC;
(2)∵PM⊥AD,PN⊥CD,
∴∠PMD=∠PND=90°,
∵∠ADC=90°,
∴四边形PMDN是矩形,
∵PM=PN,
∴四边形MPND是正方形.
点评 此题主要考查了正方形的判定,以及全等三角形的判定和性质,关键是掌握到角两边距离相等的点在角的平分线上,邻边相等的矩形是正方形.


 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:初中数学 来源: 题型:解答题
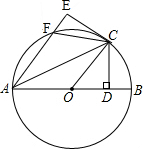 如图,AB是⊙O的直径,C是⊙O上的一点,CD⊥AB于D.△ACD沿AC翻折后点D落在点E,AE交⊙O于点F;连接OC、FC.
如图,AB是⊙O的直径,C是⊙O上的一点,CD⊥AB于D.△ACD沿AC翻折后点D落在点E,AE交⊙O于点F;连接OC、FC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | 4和16 | C. | 1或3 | D. | 16 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,铁路上A,B两站(视为直线上两点)相距14km,C,D为两村庄(可看为两个点),DA⊥AB于A,CB⊥AB于B,已知DA=8km,CB=6km,现要在铁路上建一个土特产品收购站E,使C,D两村到E站的距离相等,则E站应建在距A站多少km处?
如图所示,铁路上A,B两站(视为直线上两点)相距14km,C,D为两村庄(可看为两个点),DA⊥AB于A,CB⊥AB于B,已知DA=8km,CB=6km,现要在铁路上建一个土特产品收购站E,使C,D两村到E站的距离相等,则E站应建在距A站多少km处?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. | 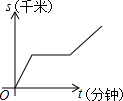 | C. | 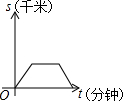 | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 作已知角的平分线 | |
| B. | 作已知线段的垂直平分线 | |
| C. | 过一点作已知直线的高 | |
| D. | 作一个角等于已知角和作一条线段等于已知线段 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com