
【题目】已知:在平面直角坐标系中,抛物线 y=ax2 -2ax+4(a<0) 交 x 轴于点 A、B,与 y 轴交于点 C,AB=6.
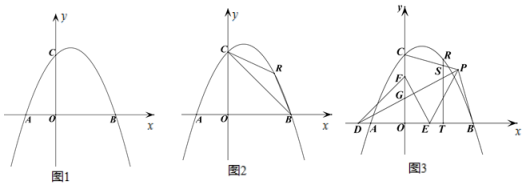
(1)如图 1,求抛物线的解析式;
(2) 如图 2,点 R 为第一象限的抛物线上一点,分别连接 RB、RC,设△RBC 的面积为 s,点 R 的横坐标为 t,求 s 与 t 的函数关系式;
(3)在(2)的条件下,如图 3,点 D 在 x 轴的负半轴上,点 F 在 y 轴的正半轴上,点 E 为 OB 上一点,点 P 为第一象限内一点,连接 PD、EF,PD 交 OC 于点 G,DG=EF,PD⊥EF,连接 PE,∠PEF=2∠PDE,连接 PB、PC,过点R 作 RT⊥OB 于点 T,交 PC 于点 S,若点 P 在 BT 的垂直平分线上,OB-TS=![]() ,求点 R 的坐标.
,求点 R 的坐标.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)R(2,4)或R(
;(3)R(2,4)或R(![]() ,
,![]() )
)
【解析】
(1)先求出抛物线的对称轴,再根据A、B关于抛物线对称轴对称和AB的长即可求出A、B的坐标,然后代入解析式即可;
(2)过点R作x轴的垂线,交BC于点M,根据题意可得点R的坐标为![]() ,点M的横坐标为t,然后求出点C的坐标,利用待定系数法求出直线BC的解析式,即可求出点M的坐标,最后利用“铅垂高,水平宽”即可求出结论;
,点M的横坐标为t,然后求出点C的坐标,利用待定系数法求出直线BC的解析式,即可求出点M的坐标,最后利用“铅垂高,水平宽”即可求出结论;
(3)设PG与EF交于点H,连接EG,设R点的坐标为![]() ,则OT=t,根据题意求出点S的坐标,即可求出直线SC的解析式,然后根据全等三角形的判定及性质、垂直平分线的判定、三线合一证出OP平分∠EOG,可得点P的横纵坐标相等,再结合已知条件即可求出点P的坐标,代入直线SC的解析式即可求出t,从而求出点R的坐标.
,则OT=t,根据题意求出点S的坐标,即可求出直线SC的解析式,然后根据全等三角形的判定及性质、垂直平分线的判定、三线合一证出OP平分∠EOG,可得点P的横纵坐标相等,再结合已知条件即可求出点P的坐标,代入直线SC的解析式即可求出t,从而求出点R的坐标.
解:(1)抛物线 y=ax2 -2ax+4(a<0)的对称轴为x=![]()
∵AB=6,A、B关于x=1对称
∴点A的横坐标为1-![]() =-2,点B的横坐标为1+
=-2,点B的横坐标为1+![]() =4
=4
∴点A的坐标为(-2,0),点B的坐标为(4,0)
将点A的坐标代入y=ax2 -2ax+4中,得
0=4a+4a+4
解得:a=![]()
∴抛物线的解析式为![]() ;
;
(2)过点R作x轴的垂线,交BC于点M
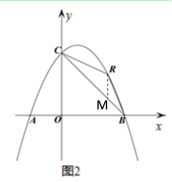
∵点 R 的横坐标为 t
∴点R的坐标为![]() ,点M的横坐标为t
,点M的横坐标为t
将x=0代入![]() 中,解得y=4
中,解得y=4
∴点C的坐标为(0,4)
设直线BC的解析式为y=kx+b
将点B、C的坐标代入,得
![]()
解得:![]()
∴直线BC的解析式为y=-x+4
∴点M的坐标为(t,-t+4)
∴RM=![]()
∴s=![]() RM·(xB-xC)=
RM·(xB-xC)=![]()
![]() ·(4-0)=
·(4-0)=![]()
(3)设PG与EF交于点H,连接EG
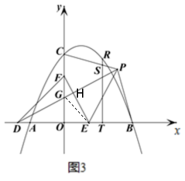
设R点的坐标为![]() ,则OT=t
,则OT=t
∵OB-TS=![]() ,OB=4
,OB=4
∴TS=![]()
∴点S的坐标为(t,![]() )
)
设直线SC的解析式为:y=mx+n
将S、C的坐标代入,得
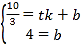
解得: 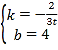
∴直线SC的解析式为![]()
∵∠DOG=∠FOE=∠DHE=90°
∴∠ODG+∠HEO=90°,∠OFE+∠HEO=90°
∴∠ODG=∠OFE
∵DG=FE
∴△ODG≌△OFE
∴OG=OE,
∴点O在GE的中垂线上,△OGE为等腰直角三角形
∴∠GEO=∠OGE=45°
∴∠PGE=∠GEO+∠PDE=45°+∠PDE,∠FEG=∠OGE-∠OFE=45°-∠PDE
∵∠PEF=2∠PDE
∴∠PEG=∠PEF+∠FEG=2∠PDE+45°-∠PDE=45°+∠PDE
∴∠PGE=∠PEG
∴PG=PE
∴点P在EG的中垂线上
∴OP垂直平分EG
∴OP平分∠EOG
∴点P的横、纵坐标相等
∵点 P 在 BT 的垂直平分线上
∴点P的坐标为(![]() )
)
将点P的坐标代入直线SC的解析式中,得
![]()
解得:![]()
经检验:![]() 均为原方程的解
均为原方程的解
当t=2时,点R的坐标为(2,4);
当t=![]() 时,点R的坐标为(
时,点R的坐标为(![]() ,
,![]() )
)
综上所述:R(2,4)或R(![]() ,
,![]() )
)


科目:初中数学 来源: 题型:
【题目】某景区内有一块矩形油菜花田地(数据如图示,单位:m.)现在其中修建一条观花道(图中阴影部分)供游人赏花.设改造后剩余油菜花地所占面积为ym2.
(1)求y与x的函数表达式;
(2)若改造后观花道的面积为13m2,求x的值;
(3)若要求 0.5≤ x ≤1,求改造后剩余油菜花地所占面积的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店老板到厂家选购![]() 、
、![]() 两种品牌的羽绒服,
两种品牌的羽绒服,![]() 品牌羽绒服每件进价比
品牌羽绒服每件进价比![]() 品牌羽绒服每件进价多
品牌羽绒服每件进价多![]() 元,若用
元,若用![]() 元购进
元购进![]() 种羽绒服的数量是用
种羽绒服的数量是用![]() 元购进
元购进![]() 种羽绒服数量的
种羽绒服数量的![]() 倍.
倍.
(1)求![]() 、
、![]() 两种品牌羽绒服每件进价分别为多少元?
两种品牌羽绒服每件进价分别为多少元?
(2)若![]() 品牌羽绒服每件售价为
品牌羽绒服每件售价为![]() 元,
元,![]() 品牌羽绒服每件售价为
品牌羽绒服每件售价为![]() 元,服装店老板决定一次性购进
元,服装店老板决定一次性购进![]() 、
、![]() 两种品牌羽绒服共
两种品牌羽绒服共![]() 件,在这批羽绒服全部出售后所获利润不低于
件,在这批羽绒服全部出售后所获利润不低于![]() 元,则最少购进
元,则最少购进![]() 品牌羽绒服多少件?
品牌羽绒服多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
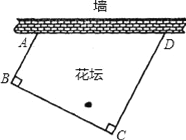
【题目】小区要用篱笆围成一个四边形花坛、花坛的一边利用足够长的墙,另三边所用的篱笆之和恰好为18米.围成的花坛是如图所示的四边形ABCD,其中∠ABC=∠BCD=90°,且BC=2AB.设AB边的长为x米.四边形ABCD面积为S平方米.
(1)请直接写出S与x之间的函数关系式(不要求写出自变量x的取值范围).
(2)当x是多少时,四边形ABCD面积S最大?最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在 10×6 的正方形网格中,每个小正方形的边长均为 1,线段 AB 的端点 A、B 均在小正方形的顶点上.
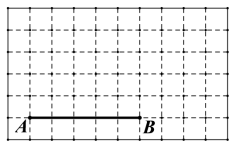
(1)在图中画出以 AB 为一腰的等腰△ABC,点 C 在小正方形顶点上,△ABC 为钝角三角形,且△ABC 的面积为![]() ;
;
(2)在图中画出以 AB 为斜边的直角三角形 ABD, 点 D在小正方形的顶点上,且 AD>BD;
(3)连接 CD,请你直接写出线段 CD 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着生活水平的提高,人们越来越注重营养健康,有一种有机水果![]() 在市场上特别受欢迎,某大型超市以10元/千克的价格在产地收购了6000千克
在市场上特别受欢迎,某大型超市以10元/千克的价格在产地收购了6000千克![]() 水果,立即将其冷藏,请根据下列信息解决问题:
水果,立即将其冷藏,请根据下列信息解决问题:
①水果![]() 的市场价每天每千克上涨0.1元;
的市场价每天每千克上涨0.1元;
②平均每天有10千克的该水果损坏,不能出售;
③每天的冷藏费用为300元;
④该水果最多保存110天;
(1)若将这批![]() 水果存放
水果存放![]() 天后一次性出售,则
天后一次性出售,则![]() 天后这批水果的销售单价为 元;
天后这批水果的销售单价为 元;
(2)将这批![]() 水果存放多少天后一次性出售所得利润为9600元?
水果存放多少天后一次性出售所得利润为9600元?
(3)将这批![]() 水果存放多少天后一次性出售可获得最大利润?最大利润是多少?
水果存放多少天后一次性出售可获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线AB与抛物线C:y=ax2+2x+c相交于点A(﹣1,0)和点B(2,3)两点.
(1)求抛物线C函数表达式;
(2)若点M是位于直线AB上方抛物线上的一动点,当![]() 的面积最大时,求此时
的面积最大时,求此时![]() 的面积S及点M的坐标.
的面积S及点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以△ABC的三条边为边,分别向外作正方形,连接EF,GH,DJ,如果△ABC的面积为8,则图中阴影部分的面积为( )

A.28B.24C.20D.16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了扎实推进精准扶贫工作,某地出台了民生兜底、医保脱贫、教育救助、产业扶持、养老托管和易地搬迁这六种帮扶措施,每户贫困户都享受了2到5种帮扶措施,现把享受了2种、3种、4种和5种帮扶措施的贫困户分别称为A、B、C、D类贫困户.为检査帮扶措施是否落实,随机抽取了若干贫困户进行调查,现将收集的数据绘制成下面两幅不完整的统计图:
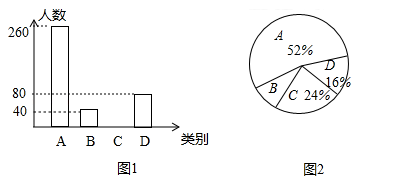
请根据图中信息回答下面的问题:
(1)本次抽样调查了多少户贫困户?
(2)抽查了多少户C类贫困户?并补全统计图;
(3)若该地共有13000户贫困户,请估计至少得到4项帮扶措施的大约有多少户?
(4)为更好地做好精准扶贫工作,现准备从D类贫困户中的甲、乙、丙、丁四户中随机选取两户进行重点帮扶,请用树状图或列表法求出恰好选中甲和丁的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com