
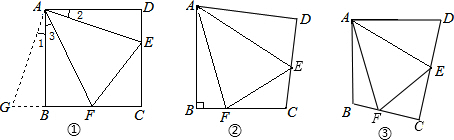
 19、填空:如图,在四边形ABCD中,∠B=∠D=90°,E是BC上一点,且∠AEC=∠BAD,试说明AE∥DC.(把下列说明补充完整)
19、填空:如图,在四边形ABCD中,∠B=∠D=90°,E是BC上一点,且∠AEC=∠BAD,试说明AE∥DC.(把下列说明补充完整) 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:初中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 填空:如图,在四边形ABCD中,∠B=∠D=90°,E是BC上一点,且∠AEC=∠BAD,试说明AE∥DC.(把下列说明补充完整)
填空:如图,在四边形ABCD中,∠B=∠D=90°,E是BC上一点,且∠AEC=∠BAD,试说明AE∥DC.(把下列说明补充完整)查看答案和解析>>
科目:初中数学 来源: 题型:
观察探究,完成说明和填空.
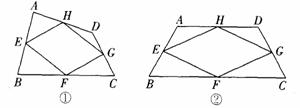
如图①,在四边形ABCD中,点E、F、G、H分别是边AB、BC、CD、DA的中点,顺次连接点E、F、G、H,得到的四边形.EFGH叫做中点四边形.
(1)试说明四边形EFGH是平行四边形;
(2)如图②,当四边形ABCD变成等腰梯形时,它的中点四边形是菱形,请你探究并填空:
当四边形ABCD变成平行四边形时,它的中点四边形是_________;
当四边形ABCD变成矩形时,它的中点四边形是_________;
当四边形ABCD变成菱形时,它的中点四边形是_________;
当四边形ABCD变成正方形时,它的中点四边形是_________.
(3)根据以上观察探究,请你总结中点四边形的形状由原四边形的什么决定的?
查看答案和解析>>
科目:初中数学 来源:广西自治区期末题 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com