
分析 (1)由题意得,每月销售量与销售单价之间的关系y=-2x+120,利润=(定价-进价)×销售量,从而列出关系式;
(2)根据方案A和方案B列不等式求出x的取值范围,根据函数的性质解答问题.
解答 解:(1)由题意这种T恤的单件利润为(x-30)元,
销售利润w=(x-30)(-2x+120)=-2x2+180x-3600;
(2)方案A:根据题意:-2x+120≥40且x≥30+5,
解得:35≤x≤40,
w=-2x2+180x-3600=-2(x-45)2+450,
因为在对称轴的左侧W随x的增大而增大,
所以当x=40时,W最大,W=-2(40-45)2+450=400,
方案B:依据题意,1.2×30≤x≤1.6×30,
解得:36≤x≤48,
W=-2(40-45)2+450
当x=45时,W最大,W=450.
建议:选择方案B,当售价定位45元时,利润最大为450元.
点评 此题考查了二次函数的实际应用以及性质,将实际问题转化为求函数最值问题,熟练掌握二次函数的性质是解决问题的关键.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源: 题型:解答题
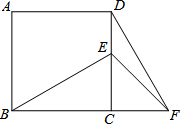 已知:如图,在正方形ABCD中,E为CD边上的一点,F为BC的延长线上一点,CE=CF.
已知:如图,在正方形ABCD中,E为CD边上的一点,F为BC的延长线上一点,CE=CF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
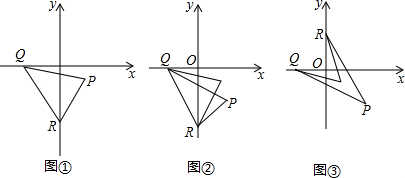
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0,1,2 | B. | 0,1 | C. | -1,-1 | D. | -1,0,1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
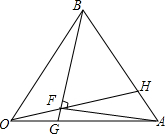 如图,等边△OAB中,G、H分别从O、A出发,以等速沿OA、AB运动,连OH、BG交于F
如图,等边△OAB中,G、H分别从O、A出发,以等速沿OA、AB运动,连OH、BG交于F查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com