解:(1)∵AE⊥BE,
∴∠AED=90°,
∵∠ADE=∠BDC,∠ACB=90°,
∴∠EAD=∠DBC,
∵在△AFC和△BDC中,

,
∴Rt△AFC≌Rt△BDC(ASA),
∴AF=BD;
(2)BD是∠ABC的平分线.
理由如下:
∵AE=

BD,
∴AF=2AE,
∵AF=AE+EF=2AE,
∴EF=AE,
∵在△AEB和△FEB中,
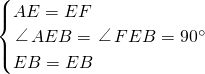
,
∴Rt△ABE≌Rt△FBE(SAS),
∴∠ABE=∠FBE,
∴BD是∠ABC的角平分线;
(3)画图:
∵△AFC与△AGC关于直线AC对称

,
∴△AFC≌△AGC,
∵△AFC≌△BDC,
∴△AGC≌△BDC,
∴DC=GC,
∵AC=BC,
∴AC-CD=CB-CG,
即AD=BG=3cm.
分析:(1)证明△AFC≌△BDC可根据全等三角形对应边相等可得AF=DB;
(2)首先证明EF=AE,再证明Rt△ABE≌Rt△FBE,可根据全等三角形对应角相等得到BD是∠ABC的平分线;
(3)首先根据题意画出图形,再根据△AFC≌△AGC,△AFC≌△BDC,可得△AGC≌△BDC,然后根据全等三角形对应边相等可得DC=GC,再利用AC=BC可得AD=BG=3cm.
点评:此题主要考查了全等三角形的判定与性质,关键是掌握全等三角形对应边相等,对应角相等.

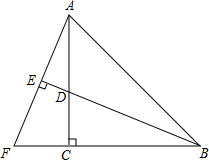 如图,在△ABC中,AC=BC,∠ACB=90°,D是AC上一点,AE⊥BD交BD的延长线于E,且AE=
如图,在△ABC中,AC=BC,∠ACB=90°,D是AC上一点,AE⊥BD交BD的延长线于E,且AE= BD,AE延长线与BC的延长线相交于F
BD,AE延长线与BC的延长线相交于F ,
, BD,
BD,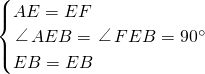 ,
, ,
,

 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为