
����Ŀ��ij��˾������ij�ֲ�Ʒÿ���ɱ�Ϊ40Ԫ�����г�����������������Ϣ���ٸò�Ʒ90��������������m������ʱ�䣨��x�죩����һ�κ�����ϵ�������������±���

�ڸò�Ʒ90����ÿ������ۼ۸���ʱ�䣨��x�죩�Ĺ�ϵ���±���

��1����m����x��һ�κ�������ʽ��
��2�������۸ò�Ʒÿ������ΪyԪ����д��y����x�ĺ�������ʽ���������90���ڸò�Ʒ������������������������Ƕ��٣�����ʾ��ÿ����������=������������ÿ�����ۼ۸�ÿ���ɱ�����
��3���ڸò�Ʒ���۵Ĺ����У����ж���������������5400Ԫ����ֱ��д�������
���𰸡���1��m=��2x+200����2�� ����40�����������������������7200Ԫ����3��46��
����40�����������������������7200Ԫ����3��46��
��������
�����������1�����ݴ���ϵ�������һ�κ�������ʽ���ɣ�
��2��������ΪyԪ����1��x��50ʱ�� ![]() ����50��x��90ʱ��
����50��x��90ʱ��![]() ���ֱ���������ϵ����ֵ���Ƚϼ��ɵõ����ۣ�
���ֱ���������ϵ����ֵ���Ƚϼ��ɵõ����ۣ�
��3��ֱ��д���ڸò�Ʒ���۵Ĺ����У�����46������������5400Ԫ��
�����������1����m��x��һ�κ���������![]() ����x=1��m=198��x=3��m=194���룬�ã�
����x=1��m=198��x=3��m=194���룬�ã�![]() ����ã�
����ã�![]() ������m����x��һ�κ�������ʽΪ
������m����x��һ�κ�������ʽΪ![]() ��
��
��2�������۸ò�Ʒÿ������ΪyԪ��y����x�ĺ�������ʽΪ�� ����1��x��50ʱ��
����1��x��50ʱ��![]() =
=![]() ������2��0������x=40ʱ��y�����ֵ�����ֵ��7200��
������2��0������x=40ʱ��y�����ֵ�����ֵ��7200��
��50��x��90ʱ��![]() ������120��0����y��x�������С������x=50ʱ��y��ֵ������ֵ��6000��
������120��0����y��x�������С������x=50ʱ��y��ֵ������ֵ��6000��
������������x=40ʱ��y��ֵ������ֵ��7200������90���ڸò�Ʒ��40�����������������������7200Ԫ��
��3���ڸò�Ʒ���۵Ĺ����У�����46������������5400Ԫ��


 ���100��1�ž�ϵ�д�
���100��1�ž�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�CD��AB������ΪD����E��BC�ϣ�EF��AB������ΪF��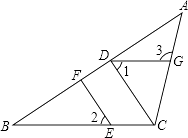
��1��CD��EFƽ������˵�����ɣ�
��2�������1=��2���ҡ�ACB=110�㣬���3�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ȷ���ǣ�������
A. 3a+2b=5ab B. 5a��2a=3a C. b2b3=b6 D. ��x+y��2=x2+y2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijƷ�ƵĹ������г���ҵΪ�˽�����ڼ����վ���������г�ʹ�������������ȷͶ�ţ������ڶ������������A��B��C��������վ��Ʒ�����г���ʹ����������ͳ�ƣ�������ͼ1��ͼ2��ʾ��ͳ��ͼ������ͼ����Ϣ����������⣺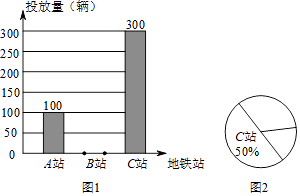
��1����Ʒ�����г������ڸ���������վ����Ͷ�������г�����
��2���벹ȫͼ1�е�����ͳ��ͼ���������Aվ��ͼ2������Ӧ��Բ�ĽǵĶ�����
��3����ͳ�����������Ʒ�Ƴ��ƻ�����Щ������Ͷ��1200���������ڵ���BվӦͶ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Ҫ����ɼ��㣺
��1���Ȼ�������ֵ����4ab3��8a2b2����4ab+��2a+b����2a��b��������a=2��b=1��
��2����ʽ�ֽ⣺3x2��6axy+3ay2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
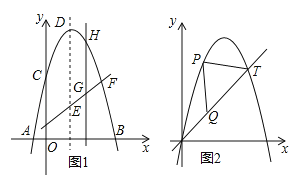
����Ŀ����ͼ1��ʾ����֪������![]() �Ķ���ΪD����x�ύ��A��B���㣬��y�ύ��C�㣬EΪ�Գ����ϵ�һ�㣬����CE�����߶�CE�Ƶ�E����ʱ�뷽����ת90���C�Ķ�Ӧ��C��ǡ������y���ϣ�
�Ķ���ΪD����x�ύ��A��B���㣬��y�ύ��C�㣬EΪ�Գ����ϵ�һ�㣬����CE�����߶�CE�Ƶ�E����ʱ�뷽����ת90���C�Ķ�Ӧ��C��ǡ������y���ϣ�
��1��ֱ��д��D���E������ꣻ
��2����FΪֱ��C��E����֪�����ߵ�һ�����㣬��H����������C��F֮���һ�����㣬������H��ֱ��HG��y��ƽ�У�����ֱ��C��E���ڵ�G�����H�ĺ�����Ϊm��0��m��4������ô��mΪ��ֵʱ��![]() =5��6��
=5��6��
��3��ͼ2��ʾ������������![]() ����ƽ��1����λ��õ��ģ���T��5��y�����������ϣ���P����������O��T֮�������һ�㣬���߶�OT���Ƿ����һ��Q��ʹ��PQT�ǵ���ֱ�������Σ������ڣ������Q�����ꣻ�������ڣ���˵�����ɣ�
����ƽ��1����λ��õ��ģ���T��5��y�����������ϣ���P����������O��T֮�������һ�㣬���߶�OT���Ƿ����һ��Q��ʹ��PQT�ǵ���ֱ�������Σ������ڣ������Q�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������y=ax2��2x��x���������ཻ�ڵ�A������ΪB��
��1���ú�a��ʽ�ӱ�ʾ��B�����ꣻ
��2��������C��0����2����ֱ��AC��OB��OΪԭ�㣩�ཻ�ڵ�D���������ߵĶԳ����ཻ�ڵ�E����OCD�ա�BED����a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ӵ�����l1��l2�ƽ�У�A��B��l1�ϵ����㣬C��D��l2�ϵ����㣬ij���ڵ�A����á�CAB=90�㣬��DAB=30�㣬����AB����ǰ��20�����E����E���߶�AB�ϣ�����á�DEB=60�㣬��C��D�����ľ��룮
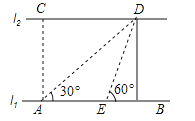
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com