
 某校的围墙上端由一段段相同的凹曲拱形栅栏组成.如图所示,其拱形为抛物线的一部分,栅栏由立柱和横杆用相同的钢筋切割而成,横杆AB间按相同的间距$\frac{1}{5}$米用5根立柱加固,OC的长为$\frac{3}{5}$米.
某校的围墙上端由一段段相同的凹曲拱形栅栏组成.如图所示,其拱形为抛物线的一部分,栅栏由立柱和横杆用相同的钢筋切割而成,横杆AB间按相同的间距$\frac{1}{5}$米用5根立柱加固,OC的长为$\frac{3}{5}$米.分析 (1)先根据题意求得A(-$\frac{3}{5}$,$\frac{3}{5}$),再设y=ax2,根据待定系数法,求得抛物线的解析式为y=$\frac{5}{3}$x2;
(2)根据(1)中的函数解析式,求得当x=-$\frac{2}{5}$,x=-$\frac{1}{5}$,x=0,x=$\frac{1}{5}$,x=$\frac{2}{5}$时,y=$\frac{4}{15}$,y=$\frac{1}{15}$,y=0,y=$\frac{1}{15}$,y=$\frac{4}{15}$,最后计算栅栏所需钢筋的总长度;
(3)先根据A(-$\frac{3}{5}$,$\frac{16}{15}$),运用待定系数法,求得抛物线的解析式为y=$\frac{80}{27}$x2,再求得当x=$\frac{2}{5}$,x=$\frac{1}{5}$时,y=$\frac{64}{135}$,y=$\frac{16}{135}$,进而计算栅栏所需钢筋的总长度.
解答 解:(1)以O点为原点,水平向右为x轴正方向,竖直向上为y轴正方向,建立直角坐标系,如图所示: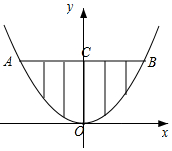
∵横杆AB间按相同的间距$\frac{1}{5}$米用5根立柱加固,OC的长为$\frac{3}{5}$米,
∴A(-$\frac{3}{5}$,$\frac{3}{5}$),
设y=ax2,则
$\frac{3}{5}$=a•(-$\frac{3}{5}$)2,
解得a=$\frac{5}{3}$,
∴抛物线的解析式为y=$\frac{5}{3}$x2;
(2)∵在y=$\frac{5}{3}$x2中,当x=-$\frac{2}{5}$,x=-$\frac{1}{5}$,x=0,x=$\frac{1}{5}$,x=$\frac{2}{5}$时,
y=$\frac{4}{15}$,y=$\frac{1}{15}$,y=0,y=$\frac{1}{15}$,y=$\frac{4}{15}$,
∴栅栏所需钢筋的总长度=5×$\frac{3}{5}$-2($\frac{4}{15}$+$\frac{1}{15}$)+$\frac{3}{5}$×2≈3.5m;
(3)由题可得A(-$\frac{3}{5}$,$\frac{16}{15}$),
设y=a'x2,则
$\frac{16}{15}$=a'•(-$\frac{3}{5}$)2,
解得a'=$\frac{80}{27}$,
∴y=$\frac{80}{27}$x2,
∴当x=$\frac{2}{5}$,x=$\frac{1}{5}$时,y=$\frac{64}{135}$,y=$\frac{16}{135}$,
∴栅栏所需钢筋的总长度=5×$\frac{16}{15}$-2($\frac{64}{135}$+$\frac{16}{135}$)+$\frac{3}{5}$×2=$\frac{722}{135}$<7,
∴一根长为7米的钢筋能做成一段符合要求的新栅栏.
点评 本题主要考查了二次函数的综合应用,解决问题的关键是掌握待定系数法求二次函数解析式的方法.在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.


科目:初中数学 来源: 题型:填空题
 如图,是由五个边长为2cm的小立方块搭成的几何体,一只蚂蚁想从A沿着这个几何体的表面爬到点B,它要爬行的最短路程应为2$\sqrt{5}$cm.
如图,是由五个边长为2cm的小立方块搭成的几何体,一只蚂蚁想从A沿着这个几何体的表面爬到点B,它要爬行的最短路程应为2$\sqrt{5}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在扇形OAB中,∠AOB=110°,将扇形OAB沿过点B的直线折叠,点O恰好落在$\widehat{AB}$上的点D处,折痕交OA于点C,则$\widehat{AD}$的度数为( )
如图,在扇形OAB中,∠AOB=110°,将扇形OAB沿过点B的直线折叠,点O恰好落在$\widehat{AB}$上的点D处,折痕交OA于点C,则$\widehat{AD}$的度数为( )| A. | 40° | B. | 50° | C. | 60° | D. | 70° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 已知抛物线y=ax2+bx+c的顶点为D(-1,3),与x轴的一个交点在(-3,0)和(-2,0)之间,其部分图象如图,则以下结论:
已知抛物线y=ax2+bx+c的顶点为D(-1,3),与x轴的一个交点在(-3,0)和(-2,0)之间,其部分图象如图,则以下结论:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
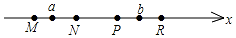 如图,M、N、P、R 分别是数轴上四个整数所对应的点,其中有一点是原点,并且 MN=NP=PR=1.数 a 对应的点在 M 与 N 之间,数 b 对应的点在 P 与 R 之间,若|a|+|b|=3,则原点是M或R(M、N、P、R中选)
如图,M、N、P、R 分别是数轴上四个整数所对应的点,其中有一点是原点,并且 MN=NP=PR=1.数 a 对应的点在 M 与 N 之间,数 b 对应的点在 P 与 R 之间,若|a|+|b|=3,则原点是M或R(M、N、P、R中选)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com