
分析 通过分母有理化化简x、y,然后代入求值.
解答 解:x=$\frac{\sqrt{3}-\sqrt{2}}{\sqrt{3}+\sqrt{2}}$=($\sqrt{3}-\sqrt{2}$)2=5-2$\sqrt{6}$,y=$\frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}-\sqrt{2}}$=($\sqrt{3}$+$\sqrt{2}$)2=5+2$\sqrt{6}$,
所以3x2-5xy+3y2
=3(x2+y2)-5xy
=3[(5-2$\sqrt{6}$)2+(5+2$\sqrt{6}$)2]-5(5+2$\sqrt{6}$)(5-2$\sqrt{6}$)
=3[52+(2$\sqrt{6}$)2]-5×[52-(2$\sqrt{6}$)2]
=3(25+24)-5×(25-24)
=3×49-5
=142.
点评 本题考查了二次根式的化简求值.掌握分母有理化是解答该题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
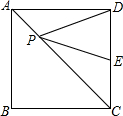 如图,在正方形ABCD中,AB=9,点E在CD边上,且DE=2CE,点P是对角线AC上的一个动点,则PE+PD的最小值是( )
如图,在正方形ABCD中,AB=9,点E在CD边上,且DE=2CE,点P是对角线AC上的一个动点,则PE+PD的最小值是( )| A. | 3$\sqrt{10}$ | B. | 10$\sqrt{3}$ | C. | 9 | D. | 9$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
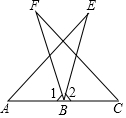 如图,已知AB=CB,BE=BF,点A,B,C在同一条直线上,∠1=∠2.
如图,已知AB=CB,BE=BF,点A,B,C在同一条直线上,∠1=∠2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
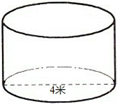 有一个圆柱形的蓄水池底面直径为4米,深为2.5米.
有一个圆柱形的蓄水池底面直径为4米,深为2.5米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
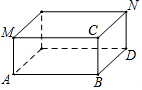 如图,有一个长方体无盖的盒子,长AB=8cm,宽BD=5cm,高BC=1cm,一只蚂蚁经过盒子里面从N爬到M.
如图,有一个长方体无盖的盒子,长AB=8cm,宽BD=5cm,高BC=1cm,一只蚂蚁经过盒子里面从N爬到M.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com