
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() 交
交![]() 于
于![]() ,
,![]() 是
是![]() 上一点,
上一点,![]() 为
为![]() 内心,
内心,![]() 交
交![]() 于
于![]() ,且
,且![]() .
.

(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)求证:![]() .
.
【答案】见解析
【解析】
(1)利用三角形内心性质得∠EBD=∠CBD.加上∠DBE=∠BAD,则∠CBD=∠BAD,根据圆周角定理得到∠BDA=90°.然后证明∠ABC=90°.于是根据切线的判定定理可判断BC是⊙O的切线;
(2)连接ED,如图,则∠BED=∠CED,再证明∠EFD=∠EGD,从而可判断△DFE≌△DGE.于是得到DF=DG.
(1)∵点D为△BCE的内心,
∴BD平分∠EBC.
∴∠EBD=∠CBD.
又∵∠DBE=∠BAD,
∴∠CBD=∠BAD.
又∵AB是〇O直径,
∴∠BDA=90°.
在Rt△BAD中,∠BAD+∠ABD=90°,
∴∠CBD+∠ABD=90°,即∠ABC=90°.
∴BC⊥AB.
又∵AB为直径,
∴BC是〇O的切线;
(2)连接ED,如图,

则ED平分∠BEC,
∴∠BED=∠CED.
∵∠EFD为△BFD的外角
∴∠EFD=∠ADB+∠EBD=90°+∠EBD,
又∵四边形ABDG为圆的内接四边形,
∴∠EGD=180°∠ABD=180°(90°∠CBD)=90°+∠CBD,
又∵∠EBD=∠CBD,
∴∠EFD=∠EGD
又∵ED=ED,
∴△DFE≌△DGE(AAS ).
∴DF=DG.


科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,矩形ABCD的边AB:BC=3:2,点A(3,0),B(0,6)分别在x轴,y轴上,反比例函数![]() (x>0)的图像经过点D,则
(x>0)的图像经过点D,则![]() 值为( )
值为( )
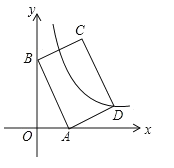
A. ﹣14 B. 14 C. 7 D. ﹣7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场欲购进果汁饮料和碳酸饮料共60箱,两种饮料每箱的进价和售价如下表所示。设购进果汁饮料x箱(x为正整数),且所购进的两种饮料能全部卖出,获得的总利润为W元(注:总利润=总售价-总进价)。
(1)设商场购进碳酸饮料y箱,直接写出y与x的函数解析式;
(2)求总利润w关于x的函数解析式;
(3)如果购进两种饮料的总费用不超过2100元,那么该商场如何进货才能获利最多?并求出最大利润。
饮料 | 果汁饮料 | 碳酸饮料 |
进价(元/箱) | 40 | 25 |
售价(元/箱) | 52 | 32 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形![]() 是矩形,
是矩形,![]() ,
,![]() ,动点
,动点![]() 以每秒4个单位的速度从点
以每秒4个单位的速度从点![]() 沿线段
沿线段![]() 向
向![]() 点运动,同时动点
点运动,同时动点![]() 以每秒6个单位的速度从点
以每秒6个单位的速度从点![]() 出发沿
出发沿![]() 的方向运动,当点
的方向运动,当点![]() 到达点
到达点![]() 时,
时,![]() 、
、![]() 同时停止运动,若记
同时停止运动,若记![]() 的面积为
的面积为![]() ,运动时间为
,运动时间为![]() ,则下列图象中能大致表示,
,则下列图象中能大致表示,![]() 与
与![]() 之间函数关系图象的是( )
之间函数关系图象的是( )

A. B.
B.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
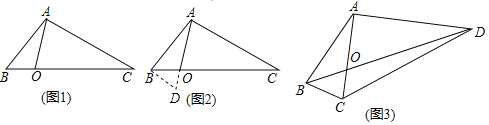
【题目】(1)某学校“智慧方园”数学社团遇到这样一个题目:
如图1,在△ABC中,点O在线段BC上,∠BAO=30°,∠OAC=75°,AO=![]() ,BO:CO=1:3,求AB的长.
,BO:CO=1:3,求AB的长.
经过社团成员讨论发现,过点B作BD∥AC,交AO的延长线于点D,通过构造△ABD就可以解决问题(如图2).
请回答:∠ADB= °,AB= .
(2)请参考以上解决思路,解决问题:
如图3,在四边形ABCD中,对角线AC与BD相交于点O,AC⊥AD,AO=![]() ,∠ABC=∠ACB=75°,BO:OD=1:3,求DC的长.
,∠ABC=∠ACB=75°,BO:OD=1:3,求DC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形DEFG的顶点D、E在△ABC的边BC上,顶点G、F分别在边AB、AC上.如果BC=4,△ABC的面积是6,那么这个正方形的边长是_____.
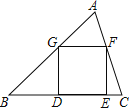
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,设二次函数![]() ,其中
,其中![]() .
.
(1)若函数![]() 的图象经过点(2,6),求函数
的图象经过点(2,6),求函数![]() 的表达式;
的表达式;
(2)若一次函数![]() 的图象与
的图象与![]() 的图象经过x轴上同一点,探究实数
的图象经过x轴上同一点,探究实数![]() ,
,![]() 满足的关系式;
满足的关系式;
(3)已知点![]() 和
和![]() 在函数
在函数![]() 的图象上,若
的图象上,若![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com