
【题目】如图,抛物线y1=a(x+2)2﹣3与y2= ![]() (x﹣3)2+1交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.则以下结论: ①无论x取何值,y2的值总是正数;
(x﹣3)2+1交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.则以下结论: ①无论x取何值,y2的值总是正数;
②a=1;
③当x=0时,y2﹣y1=4;
④2AB=3AC;
其中正确结论是( )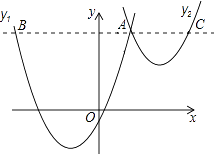
A.①②
B.②③
C.③④
D.①④
【答案】D
【解析】解:①∵抛物线y2= ![]() (x﹣3)2+1开口向上,顶点坐标在x轴的上方,∴无论x取何值,y2的值总是正数,故本小题正确;②把A(1,3)代入,抛物线y1=a(x+2)2﹣3得,3=a(1+2)2﹣3,解得a=
(x﹣3)2+1开口向上,顶点坐标在x轴的上方,∴无论x取何值,y2的值总是正数,故本小题正确;②把A(1,3)代入,抛物线y1=a(x+2)2﹣3得,3=a(1+2)2﹣3,解得a= ![]() ,故本小题错误;③由两函数图象可知,抛物线y1=a(x+2)2﹣3解析式为y1=
,故本小题错误;③由两函数图象可知,抛物线y1=a(x+2)2﹣3解析式为y1= ![]() (x+2)2﹣3,当x=0时,y1=
(x+2)2﹣3,当x=0时,y1= ![]() (0+2)2﹣3=﹣
(0+2)2﹣3=﹣ ![]() ,y2=
,y2= ![]() (0﹣3)2+1=
(0﹣3)2+1= ![]() ,故y2﹣y1=
,故y2﹣y1= ![]() +
+ ![]() =
= ![]() ,故本小题错误;④∵物线y1=a(x+2)2﹣3与y2=
,故本小题错误;④∵物线y1=a(x+2)2﹣3与y2= ![]() (x﹣3)2+1交于点A(1,3), ∴y1的对称轴为x=﹣2,y2的对称轴为x=3,
(x﹣3)2+1交于点A(1,3), ∴y1的对称轴为x=﹣2,y2的对称轴为x=3,
∴B(﹣5,3),C(5,3)
∴AB=6,AC=4,
∴2AB=3AC,故本小题正确.
故选D.
根据与y2= ![]() (x﹣3)2+1的图象在x轴上方即可得出y2的取值范围;把A(1,3)代入抛物线y1=a(x+2)2﹣3即可得出a的值;由抛物线与y轴的交点求出,y2﹣y1的值;根据两函数的解析式直接得出AB与AC的关系即可.
(x﹣3)2+1的图象在x轴上方即可得出y2的取值范围;把A(1,3)代入抛物线y1=a(x+2)2﹣3即可得出a的值;由抛物线与y轴的交点求出,y2﹣y1的值;根据两函数的解析式直接得出AB与AC的关系即可.


科目:初中数学 来源: 题型:
【题目】如图,直线AB,CD相交于点O,OE⊥AB于O,若∠BOD=40°,则不正确的结论是( )

A.∠AOC=40° B.∠COE=130° C.∠EOD=40° D.∠BOE=90°
查看答案和解析>>
科目:初中数学 来源: 题型:
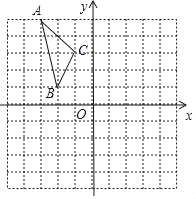
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣2,1),C(﹣1,3).
(1)画出△ABC和△A1B1C1关于原点O对称,画出△A1B1C1,并写出△A1B1C1的各顶点的坐标;
(2)将△ABC绕着点O按顺时针方向旋转90°得到的△A2B2C2,画出△A2B2C2,并写出△A2B2C2的各顶点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校“数学魔盗团”社团准备购买A,B两种魔方,已知购买2个A种魔方和6个B种魔方共需130元,购买1个A种魔方比1个B种魔方多花5元.

(1)求这两种魔方的单价;
(2)结合社员们的需求,社团决定购买A,B两种魔方共100个(其中A种魔方不超过50个).“双11期间”某商店有两种优惠活动,如图所示.请根据以上信息填空:购买A种魔方________个时选择活动一盒活动二购买所需费用相同.
查看答案和解析>>
科目:初中数学 来源: 题型:
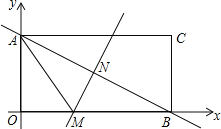
【题目】如图,长方形AOBC在直角坐标系中,点A在y轴上,点B在x轴上,已知点C的坐标是(8,4).
(1)对角线AB的垂直平分线MN交x轴于点M,连接AM,求线段AM的长;
(2)在x轴上是否存在一个点P,使△PAM为等腰三角形?如果有请直接写出符合题意的所有点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ABCD中,AB=10,BC=3,E为AB边的中点,P为CD边上的点,且△AEP是腰长为5的等腰三角形,则DP=_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工人计划加工一批产品,如果每小时加工产品10个,就可以在预定时间完成任务,如果每小时多加工2个,就可以提前1小时完成任务.
(1)该产品的预定加工时间为几小时?
(2)若该产品销售时的标价为100元/个,按标价的八折销售时,每个仍可以盈利25元,该批产品总成本为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料,解答后面的问题.
解方程:![]() -
-![]() =0.
=0.
解:设y=![]() ,则原方程可化为y-
,则原方程可化为y-![]() =0,方程两边同时乘y,得y2-4=0,解得y1=2,y2=-2.
=0,方程两边同时乘y,得y2-4=0,解得y1=2,y2=-2.
经检验,y1=2,y2=-2都是方程y-![]() =0的解.
=0的解.
当y=2时,![]() =2,解得x=-1;当y=-2时,
=2,解得x=-1;当y=-2时,![]() =-2,解得x=
=-2,解得x=![]() .
.
经检验,x1=-1,x2=![]() 都是原分式方程的解.所以原分式方程的解为x1=-1,x2=
都是原分式方程的解.所以原分式方程的解为x1=-1,x2=![]() .
.
上述这种解分式方程的方法称为换元法.
问题:
(1)若在方程![]() -
-![]() =0中,设y=
=0中,设y=![]() ,则原方程可化为________________;
,则原方程可化为________________;
(2)若在方程![]() -
-![]() =0中,设y=
=0中,设y=![]() ,则原方程可化为________________;
,则原方程可化为________________;
(3)模仿上述换元法解方程:![]() -
-![]() -1=0.
-1=0.
查看答案和解析>>
科目:初中数学 来源: 题型:
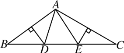
【题目】如图,在△ABC中,AB的垂直平分线交BC于点D,AC的垂直平分线交BC于点E,连接AD,AE.
(1)若∠BAC=110°,求∠DAE的度数;
(2)若∠BAC=θ(0°<θ<180°),求∠DAE的度数.(用含θ的式子表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com