
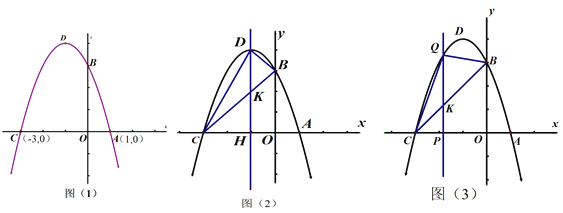
【题目】已知,如图,抛物线与x轴交点坐标为A(1,0),C(-3,0),
(1)若已知顶点坐标D为(-1,4)或B点(0,3),选择适当方式求抛物线的解析式.
(2)若直线DH为抛物线的对称轴,在(1)的基础上,求线段DK的长度,并求△DBC的面积.
(3)将图(2)中的对称轴向左移动,交x轴于点p(m,0)(-3<m<-1),与线段BC、抛物线的交点分别为点K、Q,用含m的代数式表示QK的长度,并求出当m为何值时,△BCQ的面积最大?
【答案】(1)y=-x2-2x+3;(2)3; (3)m=-![]() 时,面积最大.
时,面积最大.
【解析】试题分析:(1)用待定系数法求函数关系式即可;
(2)先根据![]() 得KH=2,所以DK=2,S△DBC=
得KH=2,所以DK=2,S△DBC=![]() DK×OC即可;
DK×OC即可;
(3)先根据QK=QK-KP求出QK=-m2-3m,再由S△BCQ=![]() QK×|OC|得出结果即可.
QK×|OC|得出结果即可.
试题解析:(1)设二次函数解析式为y=a(x+1)2+4
将B(0,3)代入,得a=-1,
∴二次函数解析式为y=-x2-2x+3;
(2)易得DH∥OB,
∴KH:OB=CH:CO
∵C(-3,0),B(0,3)且直线DH是抛物线的对称轴,
∴CH=2,CO=3,OB=3
∴CH=2
∵D(-1,4)
∴DH=4,
∴DK=DH-KH=4-2=2;
∴S△DBC=![]() DK×OC=
DK×OC=![]() ×2×3=3
×2×3=3
(3)QK=QK-KP=-m2-2m+3-(m+3)=-m2-3m.
S△BCQ=![]() QK×|OC|=
QK×|OC|=![]() (-m2-3m)×3=--
(-m2-3m)×3=-- ![]() .
.
∴当m=![]() =-
=-![]() 时,面积最大.
时,面积最大.


科目:初中数学 来源: 题型:
【题目】“书香长沙2019世界读书日”系列主题活动激发了学生的阅读兴趣,我校为满足学生的阅读需求,欲购进一批学生喜欢的图书,学校组织学生会成员随机抽取部分学生进行问卷调查,被调查学生须从“文史类、杜科类、小说类、生活类”中选择自己喜欢的一类,根据调查结果绘制了统计图(未完成),请根据图中信息,解答下列问题:
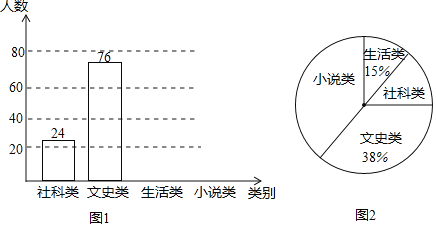
(1)此次共调查了 名学生;
(2)将条形统计图补充完整;
(3)图2中“小说类”所在扇形的圆心角为 度;
(4)若该校共有学生3000人,估计该校喜欢“文史类”书籍的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为鼓励大学毕业生自主创业,某市政府出台了相关政策:由政府协调,本市企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担.李明按照相关政策投资销售本市生产的一种新型节能灯.已知这种节能灯的成本价为每件10元,出厂价为每件12元,每月销售量y(件)与销售单价x(元)之间的关系近似满足一次函数:y=-10x+500.
(1)李明在开始创业的第一个月将销售单价定为20元,那么政府这个月为他承担的总差价为多少元?
(2)设李明获得的利润为W(元),当销售单价定为多少元时,每月可获得最大利润?
(3)物价部门规定,这种节能灯的销售单价不得高于25元.如果李明想要每月获得的利润不低于3000元,那么政府为他承担的总差价最少为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)(2a+1)2-(2a+1)(-1+2a) (2)2006×2008-20072
(3)(x-y)3·(x-y)2·(y-x) (4)(3mn+1)(3mn-1)-8m2n2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列条件中:①∠A+∠B=∠C,②∠A:∠B:∠C=1: 2:3,③∠A=90°﹣∠B,④∠A=∠B=∠C中,能确定△ABC是直角三角形的条件有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足,连接CD,且交OE于点F.
(1)求证:OE是CD的垂直平分线.
(2)若∠AOB=60,请你探究OE,EF之间有什么数量关系?并证明你的结论。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.
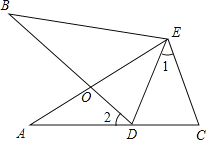
(1)求证:∠BDE=∠C;
(2)求证:△AEC≌△BED;
(3)若∠2=40°,则∠BDE=______°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列解题过程:
 =
= =
=![]() =
=![]() -2;
-2;
 =
= =
=![]() .
.
请回答下列问题:
(1)观察上面的解题过程,请直接写出式子![]() = ;
= ;
(2)观察上面的解题过程,请直接写出式子![]() = ;
= ;
(3)利用上面所提供的解法,请求![]() +···+
+···+![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com