
 如图Rt△ABC的外接圆⊙O,∠ACB=90°,∠ACB的平分线交⊙O于D.
如图Rt△ABC的外接圆⊙O,∠ACB=90°,∠ACB的平分线交⊙O于D.分析 (1)先根据勾股定理求出斜边AB=10,由90°的圆周角所对的弦是直径得:AB是⊙O的直径,所以可求得半径的长,再利用角平分线得圆周角相等:∠ACD=∠BCD,则△ADB是等腰直角三角形,由此可求得AD和BD的长;
(2)如图1,作辅助线,构建全等三角形,先证明△ACE和△BCF是等腰直角三角形,则AC=$\sqrt{2}$AE=$\sqrt{2}$EC,BC=$\sqrt{2}$BF=$\sqrt{2}$FC,再证明△AED≌△DFB,得DE=BF,代入所求的式子$\frac{AC+BC}{CD}$计算即可;
如图2,先根据直角三角形内切圆的半径公式得:IG=$\frac{AC+BC-AB}{2}$,变形后再把图1的结论代入可求得结论.
解答 解:(1)∵∠ACB=90°,
∴AB是⊙O的直径,
由勾股定理得:AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∴⊙O的半径R为5cm,
∵AB是⊙O的直径,
∴∠ADB=90°,
∵CD平分∠ACB,
∴∠ACD=∠BCD,
∴AD=BD,
设AD=xcm,
由勾股定理得:AB2=AD2+BD2,
则2x2=102,
x=±5$\sqrt{2}$,
∴AD=BD=5$\sqrt{2}$cm;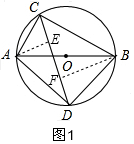
(2)如图1,过A作AE⊥CD于E,过B作BF⊥CD于F,
∵∠ACD=∠BCD=45°,
∴△ACE和△BCF是等腰直角三角形,
∴AC=$\sqrt{2}$AE=$\sqrt{2}$EC,
BC=$\sqrt{2}$BF=$\sqrt{2}$FC,
∵∠ADB=90°,
∴∠ADC+∠BDC=90°,
∵∠AED=90°,
∴∠ADC+∠EAD=90°,
∴∠BDC=∠EAD,
∵AD=BD,∠AED=∠BFD=90°,
∴△AED≌△DFB,
∴DE=BF,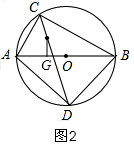
∴AE=EC=DF,
∴AC=$\sqrt{2}$CE,BC=$\sqrt{2}$DE,
∴$\frac{AC+BC}{CD}$=$\frac{\sqrt{2}CE+\sqrt{2}DE}{CD}$=$\sqrt{2}$;
∴当点C在⊙O移动(但不与A、B重合),$\frac{AC+BC}{CD}$的值不发生变化,等于$\sqrt{2}$;
如图2,I为△ABC内心,IG⊥AB,
∴IG是△ABC内切圆的半径,
则IG=$\frac{AC+BC-AB}{2}$,
AB+2IG=AC+BC,
由图1得:AC+BC=$\sqrt{2}$CD,
∴$\frac{AB+2IG}{CD}$=$\frac{AC+BC}{CD}$=$\frac{\sqrt{2}CD}{CD}$=$\sqrt{2}$.
点评 本题考查了直角三角形的外接圆和内切圆的性质,明确:①90°的圆周角所对的弦是直径,②在同圆或等圆中,相等的圆周角所对的弦相等,③直角三角形内切圆的半径r=$\frac{a+b-c}{2}$(a、b分别是直角三角形的两条直角边,c是斜边);同时构建全等三角形,利用全等三角形的对应边相等及等腰直角三角形边的倍数关系代入所求的线段的比中,得出结论.


科目:初中数学 来源: 题型:解答题
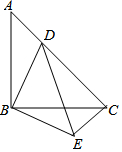 等腰Rt△ABC中,BA=BC,∠ABC=90°,将△ABD绕点B顺时针旋转90°后,得到△CBE.若AB=6,CD=2AD,求DE的长.
等腰Rt△ABC中,BA=BC,∠ABC=90°,将△ABD绕点B顺时针旋转90°后,得到△CBE.若AB=6,CD=2AD,求DE的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
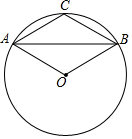 如图,已知AB为⊙O的弦长,且AB:AO=$\sqrt{3}$,点C为$\widehat{AB}$的中点,试猜想四边形AOBC的形状,并说明理由.
如图,已知AB为⊙O的弦长,且AB:AO=$\sqrt{3}$,点C为$\widehat{AB}$的中点,试猜想四边形AOBC的形状,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 等腰Rt△ABC中,∠BAC=90°,AB=AC,点A、C分别在y轴、x轴上且点A,点C的坐标分别为A(0,a),C(b,0),满足a2+b2-4a-10b+29=0.
等腰Rt△ABC中,∠BAC=90°,AB=AC,点A、C分别在y轴、x轴上且点A,点C的坐标分别为A(0,a),C(b,0),满足a2+b2-4a-10b+29=0.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
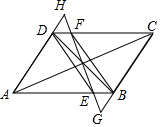 如图,已知?ABCD的对角线AC与BD相交于点O,过点O的直线与AB,DC分别交于点E,F
如图,已知?ABCD的对角线AC与BD相交于点O,过点O的直线与AB,DC分别交于点E,F查看答案和解析>>
科目:初中数学 来源: 题型:解答题
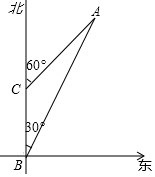 已知海岛A的周围6km的范围内有暗礁,一艘海轮在B处测得海岛A在北偏东30°的方向;向正北方向航行6km到达C处,又测得该岛在北偏东60°的方向,如果海轮不改变航向,继续向正北航行,有没有触礁的危险?
已知海岛A的周围6km的范围内有暗礁,一艘海轮在B处测得海岛A在北偏东30°的方向;向正北方向航行6km到达C处,又测得该岛在北偏东60°的方向,如果海轮不改变航向,继续向正北航行,有没有触礁的危险?查看答案和解析>>
科目:初中数学 来源:2016-2017学年浙江省七年级3月月考数学试卷(解析版) 题型:单选题
下列说法正确的个数有 ( )
①不相交的两条直线是平行线;②在同一平面内,两条直线的位置关系要么相交要么平行;③若线段AB与CD没有交点,则AB∥CD;④若a∥b,b∥c,则a与c不相交.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com