
 如图是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形,如果大正方形的面积是13,小正方形的面积是1,那么每个直角三角形的周长为$5+\sqrt{13}$.
如图是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形,如果大正方形的面积是13,小正方形的面积是1,那么每个直角三角形的周长为$5+\sqrt{13}$. 分析 根据勾股定理可以求得a2+b2等于大正方形的面积,然后求四个直角三角形的面积,即可得到ab的值,然后根据(a+b)2=a2+2ab+b2即可求解,然后得出a,b的值即可.
解答 解:根据勾股定理可得a2+b2=13,
四个直角三角形的面积是:$\frac{1}{2}$ab×4=13-1=12,即:2ab=12
则(a+b)2=a2+2ab+b2=13+12=25,
可得:$\left\{\begin{array}{l}{a+b=5}\\{ab=6}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=2}\\{b=3}\end{array}\right.$,
所以c=$\sqrt{{2}^{2}+{3}^{2}}=\sqrt{13}$,
所以周长为$5+\sqrt{13}$.
故答案为:$5+\sqrt{13}$.
点评 本题考查勾股定理,以及完全平方式,正确根据图形的关系求得a2+b2和ab的值是关键.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:选择题
 如图,△ABC中边AB的垂直平分线分别交BC、AB于点D、E,AE=4cm,△ADC的周长为12cm,则△ABC的周长是( )
如图,△ABC中边AB的垂直平分线分别交BC、AB于点D、E,AE=4cm,△ADC的周长为12cm,则△ABC的周长是( )| A. | 18cm | B. | 20cm | C. | 15cm | D. | 17cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,△ABC、△ADE中,C、D两点分别在AE、AB上,BC与DE相交于F点.若BD=CD=CE,∠ADC+∠ACD=104°,则∠DFC的度数为( )
如图,△ABC、△ADE中,C、D两点分别在AE、AB上,BC与DE相交于F点.若BD=CD=CE,∠ADC+∠ACD=104°,则∠DFC的度数为( )| A. | 104° | B. | 118° | C. | 128° | D. | 136° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
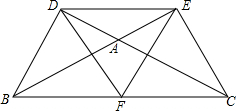 如图,在△ABC中,∠BAC>90°,DC⊥DB,BE⊥EC,F为BC上的一个动点,猜想:当F为于BC上的什么位置时,△FDE是等腰三角形,并证明你的猜想是正确的.
如图,在△ABC中,∠BAC>90°,DC⊥DB,BE⊥EC,F为BC上的一个动点,猜想:当F为于BC上的什么位置时,△FDE是等腰三角形,并证明你的猜想是正确的.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com