
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCжаЃЌЁЯC=90ЁуЃЌAB=10ЃЌAC=6ЃЎЖЏЕуPЁЂQДгЕуAЭЌЪБГіЗЂЃЌЕуPвдУПУы5ИіЕЅЮЛЕФЫйЖШбиБпABЯђжеЕуBдШЫйдЫЖЏЃЎЕуQбиелЯпACЁњCBЯђжеЕуBдШЫйдЫЖЏЃЌдкACЁЂCBЩЯЕФЫйЖШЗжБ№ЪЧУПУы6ИіЕЅЮЛЁЂУПУы8ИіЕЅЮЛЃЎвдPQЮЊБпзїе§ЗНаЮPQMNЃЌЪЙЕУЕуMгыЕуCЪМжедкPQЕФЭЌВрЃЎЩшЕуPдЫЖЏЕФЪБМфЮЊtЃЈsЃЉЃЎ
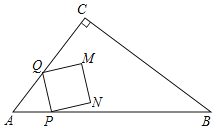
ЃЈ1ЃЉЕБЕуQдкБпACЩЯЪБЃЌгУКЌtЕФДњЪ§ЪНБэЪОPQЕФГЄЃЎ
ЃЈ2ЃЉЕБЕуMТфдкБпBCЩЯЪБЃЌЧѓtЕФжЕЃЎ
ЃЈ3ЃЉЕБЕуQдкБпACЩЯЪБЃЌЩше§ЗНаЮPQMNгыЁїABCжиЕўВПЗжЭМаЮЕФУцЛ§ЮЊSЃЌЧѓSгыtжЎМфЕФКЏЪ§ЙиЯЕЪНЃЎ
ЃЈ4ЃЉЕБе§ЗНаЮPQMNЕФБпQMБЛЁїABCЕФБпЦНЗжЪБЃЌжБНгаДГіtЕФжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉPQ =5tЃЛЃЈ2ЃЉЕБЕуMТфдкBCЩЯЪБЃЌtЕФжЕЮЊ![]() ЃЛЃЈ3ЃЉS=25t2ЃЛ
ЃЛЃЈ3ЃЉS=25t2ЃЛ![]() ЃЛ
ЃЛ![]() ЃЛЃЈ4ЃЉТњзуЬѕМўЕФtЕФжЕЮЊ
ЃЛЃЈ4ЃЉТњзуЬѕМўЕФtЕФжЕЮЊ![]() Лђ
Лђ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉШчЭМ1жаЃЌзїPEЁЭACгкEЃЎжЄУїPQЃНPAМДПЩНтОіЮЪЬтЃЎ
ЃЈ2ЃЉШчЭМ2жаЃЌжЄУїЁЯMQCЃНЁЯBЃЌИљОнcosЁЯMQCЃНcosЁЯBЃЌЙЙНЈЗНГЬМДПЩНтОіЮЪЬтЃЎ
ЃЈ3ЃЉЗжШ§жжЧщаЮЃКЂйЕБ0ЃМtЁм![]() ЪБЃЌжиЕўВПЗжЪЧе§ЗНаЮPQMNЃЎЂкЕБ
ЪБЃЌжиЕўВПЗжЪЧе§ЗНаЮPQMNЃЎЂкЕБ![]() ЃМtЁм
ЃМtЁм![]() ЪБЃЌШчЭМ3Љ2жаЃЌжиЕўВПЗжЪЧЮхБпаЮPQTRNЃЎЂлЕБ
ЪБЃЌШчЭМ3Љ2жаЃЌжиЕўВПЗжЪЧЮхБпаЮPQTRNЃЎЂлЕБ![]() ЃМtЁм1ЪБЃЌжиЕўВПЗжЪЧЫФБпаЮPQTRЃЌЗжБ№ЧѓНтМДПЩНтОіЮЪЬтЃЎ
ЃМtЁм1ЪБЃЌжиЕўВПЗжЪЧЫФБпаЮPQTRЃЌЗжБ№ЧѓНтМДПЩНтОіЮЪЬтЃЎ
ЃЈ4ЃЉЗжСНжжЧщаЮЃКЂйШчЭМ4Љ1жаЃЌЕБQTЃНTMЪБЃЌгЩcosЁЯCQTЃН![]() ЃЌЙЙНЈЗНГЬМДПЩНтОіЮЪЬтЃЎЂкШчЭМ4Љ2жаЃЌЕБMTЃНTQЪБЃЌгЩsinЁЯCTQЃН
ЃЌЙЙНЈЗНГЬМДПЩНтОіЮЪЬтЃЎЂкШчЭМ4Љ2жаЃЌЕБMTЃНTQЪБЃЌгЩsinЁЯCTQЃН![]() ЃЌЙЙНЈЗНГЬМДПЩНтОіЮЪЬтЃЎ
ЃЌЙЙНЈЗНГЬМДПЩНтОіЮЪЬтЃЎ
НтЃКЃЈ1ЃЉШчЭМ1жаЃЌзїPEЁЭACгкEЃЎ
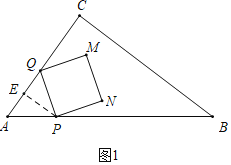
дкRtЁїABCжаЃЌЁпAB=10ЃЌAC=6ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁпЁЯPEA=ЁЯC=90ЁуЃЌ
ЁрPEЁЮBCЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрAE=3tЃЌ
ЁпAQ=6tЃЌ
ЁрAE=EQ=3tЃЌ
ЁрPEДЙжБЦНЗжЯпЖЮAQЃЌ
ЁрPQ=PA=5tЃЎ
ЃЈ2ЃЉШчЭМ2жаЃЌЕБЕуMТфдкBCЩЯЪБЃЌ
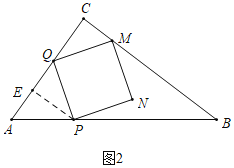
ЁпЫФБпаЮPQMNЪЧе§ЗНаЮЃЌ
ЁрMQ=PQ=5tЃЌЁЯMQP=90ЁуЃЌ
ЁрЁЯAQP+ЁЯMQC=90ЁуЃЌЁпЁЯA+ЁЯB=90ЁуЃЌЁЯA=ЁЯAQPЃЌ
ЁрЁЯMQC=ЁЯBЃЌ
ЁрcosЁЯMQC=cosЁЯBЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
НтЕУ![]() ЃЎ
ЃЎ
ЁрЕБЕуMТфдкBCЩЯЪБЃЌtЕФжЕЮЊ![]() ЃЎ
ЃЎ
ЃЈ3ЃЉЂйЕБ![]() ЪБЃЌжиЕўВПЗжЪЧе§ЗНаЮPQMNЃЌS=25t2ЃЎ
ЪБЃЌжиЕўВПЗжЪЧе§ЗНаЮPQMNЃЌS=25t2ЃЎ
ЂкЕБЕуNТфдкBCЩЯЪБЃЌШчЭМ3-1жаЃЌзїQGЁЭABгкGЃЌNHЁЭABгкHЃЌдђЁїQGPЁеЁїHPNЃЈAASЃЉЃЌПЩЕУQG=PHЃЌPG=NHЃЎ
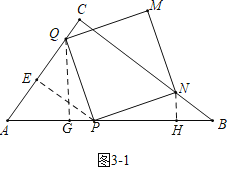
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ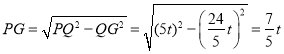 ЃЌ
ЃЌ
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
НтЕУ![]() ЃЌ
ЃЌ
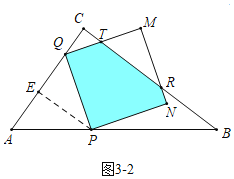
ЁрЕБ![]() ЪБЃЌШчЭМ3-2жаЃЌжиЕўВПЗжЪЧЮхБпаЮPQTRNЃЌ
ЪБЃЌШчЭМ3-2жаЃЌжиЕўВПЗжЪЧЮхБпаЮPQTRNЃЌ
![]()
![]() ЃЎ
ЃЎ
ЂлЕБ![]() ЪБЃЌжиЕўВПЗжЪЧЫФБпаЮPQTRЃЌ
ЪБЃЌжиЕўВПЗжЪЧЫФБпаЮPQTRЃЌ
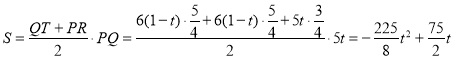 ЃЎ
ЃЎ
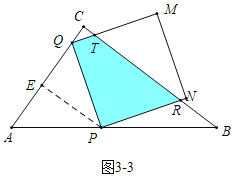
ЃЈ4ЃЉШчЭМ4-1жаЃЌЕБQT=TMЪБЃЌгЩ![]() ЃЌПЩЕУ
ЃЌПЩЕУ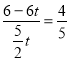 ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЎ
ЃЎ
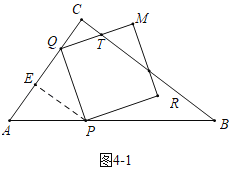
ШчЭМ4-2жаЃЌЕБMT=TQЪБЃЌгЩ![]() ЃЌПЩЕУ
ЃЌПЩЕУ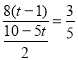 ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЎ
ЃЎ
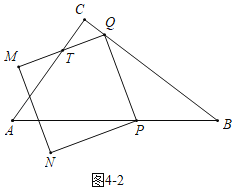
злЩЯЫљЪіЃЌТњзуЬѕМўЕФtЕФжЕЮЊ![]() Лђ
Лђ![]() ЃЎ
ЃЎ


 аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ ФПБъВтЪдЯЕСаД№АИ
ФПБъВтЪдЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкABCDжаЃЌACЃЌBDНЛгкЕуOЃЌЧвAOЃНBOЃЎ
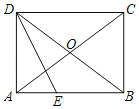
ЃЈ1ЃЉЧѓжЄЃКЫФБпаЮABCDЪЧОиаЮЃЛ
ЃЈ2ЃЉЁЯADBЕФНЧЦНЗжЯпDEНЛABгкЕуEЃЌЕБADЃН3ЃЌtanЁЯCABЃН![]() ЪБЃЌЧѓAEЕФГЄЃЎ
ЪБЃЌЧѓAEЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМзЁЂввСНШЫНјааУўХЦгЮЯЗЃЌЯжгаШ§еХаЮзДДѓаЁЭъШЋЯрЭЌЕФХЦЃЌе§УцЗжБ№БъгаЪ§зж![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌНЋШ§еХХЦБГУцГЏЩЯЃЌЯДдШКѓЗХдкзРзгЩЯЃЎ
ЃЌНЋШ§еХХЦБГУцГЏЩЯЃЌЯДдШКѓЗХдкзРзгЩЯЃЎ
ЃЈ1ЃЉМзДгжаЫцЛњГщШЁвЛеХХЦЃЌМЧТМЪ§зжКѓЗХЛиЯДдШЃЌввдйЫцЛњГщШЁвЛеХ.ЧыгУСаБэЗЈЛђЛЪїзДЭМЕФЗНЗЈаДГіЫљгаПЩФмЕФНсЙћЃЛ
ЃЈ2ЃЉШєСНШЫГщШЁЕФЪ§зжКЭЮЊ![]() ЕФБЖЪ§ЃЌдђМзЛёЪЄЃЛШєГщШЁЕФЪ§зжКЭЮЊ
ЕФБЖЪ§ЃЌдђМзЛёЪЄЃЛШєГщШЁЕФЪ§зжКЭЮЊ![]() ЕФБЖЪ§ЃЌдђввЛёЪЄЃЌетИігЮЯЗЙЋЦНТ№ЃПЧыгУИХТЪЕФжЊЪЖМгвдНтЪЭЃЎ
ЕФБЖЪ§ЃЌдђввЛёЪЄЃЌетИігЮЯЗЙЋЦНТ№ЃПЧыгУИХТЪЕФжЊЪЖМгвдНтЪЭЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
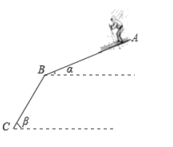
ЁОЬтФПЁП2022ФъдкББОЉНЋОйАьЕк24НьЖЌМОАТдЫЛсЃЌКмЖрбЇаЃЖМПЊеЙСЫБљбЉЯюФПбЇЯАЃЎШчЭМЃЌЛЌбЉЙьЕРгЩABЃЌBCСНВПЗжзщГЩЃЌABЃЌBCЕФГЄЖШЖМЮЊ200УзЃЌвЛЮЛЭЌбЇГЫЛЌбЉАхбиДЫЙьЕРгЩAЕуЛЌЕНСЫCЕуЃЌШєABгыЫЎЦНУцЕФМаНЧІСЮЊ20ЁуЃЌBCгыЫЎЦНУцЕФМаНЧІТЮЊ45ЁуЃЌдђЫћЯТНЕЕФИпЖШЮЊЖрЩйУзЃЎЃЈНсЙћБЃСєећЪ§ЃЉЃЈВЮПМЪ§Онsin20ЁуЁж0.342ЃЌcos20ЁуЁж0.940ЃЌtan20ЁуЁж0.364ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЬтФП:ФГаЃЦпФъМЖбЇЩњГЫГЕШЅВЮМгЩчЛсЪЕМљЛюЖЏЃЌШєУПСОПЭГЕГЫ50ШЫЃЌЛЙга12ШЫВЛФмЩЯГЕЃЛШєУПСОПЭГЕГЫ55ШЫЃЌдђзюКѓвЛСОПеСЫ8ИізљЮЛЃЌЧѓИУаЃзтетжжПЭГЕЕФСОЪ§:
ИљОнЬтвт,аЁУїЁЂаЁКьЗжБ№СаГіСЫЩаВЛЭъећЕФЗНГЬШчЯТ:
аЁУїСаГіВЛЭъећЕФЗНГЬЮЊ![]()
аЁКьСаГіВЛЭъећЕФЗНГЬЮЊ![]()
ЃЈЫЕУї:ЦфжаЁА![]() ЁББэЪОдЫЫуЗћКХ,ЁА
ЁББэЪОдЫЫуЗћКХ,ЁА![]() ЁББэЪОЪ§зжЃЉ:
ЁББэЪОЪ§зжЃЉ:
(1)аЁУїЫљСаЗНГЬжа![]() БэЪОЕФвтвхЪЧ________________________ЃЛ
БэЪОЕФвтвхЪЧ________________________ЃЛ
аЁКьЫљСаЗНГЬжа![]() БэЪОЕФвтвхЪЧ___________________________ЃЛ
БэЪОЕФвтвхЪЧ___________________________ЃЛ
(2)бЁдёСНЮЛЭЌбЇЕФЦфжавЛЮЛбЇЩњЕФзіЗЈЃЌНЋЦфВЙГфЭъећЃЌВЂЭъећЕиНтД№етЕРЬт.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЁЖжабЇЩњЬхжЪНЁПЕБъзМЁЗЙцЖЈбЇЩњЬхжЪНЁПЕЕШМЖБъзМЃК ![]() ЗжМАвдЩЯЮЊгХауЃЛ
ЗжМАвдЩЯЮЊгХауЃЛ ![]() Зж
Зж![]() ЗжЮЊСМКУЃЛ
ЗжЮЊСМКУЃЛ ![]() Зж
Зж![]() ЗжЮЊМАИёЃЛ
ЗжЮЊМАИёЃЛ![]() ЗжвдЯТЮЊВЛМАИёЃЎФГаЃЮЊСЫНтбЇЩњЕФЬхжЪНЁПЕЧщПіЃЌДгАЫФъМЖбЇЩњжаЫцЛњГщШЁСЫ
ЗжвдЯТЮЊВЛМАИёЃЎФГаЃЮЊСЫНтбЇЩњЕФЬхжЪНЁПЕЧщПіЃЌДгАЫФъМЖбЇЩњжаЫцЛњГщШЁСЫ![]() ЕФбЇЩњНјааСЫЬхжЪВтЪдЃЌВЂНЋВтЪдЪ§ОнжЦГЩШчЯТЭГМЦЭМЃЎЧыИљОнЯрЙиаХЯЂНтД№ЯТУцЕФЮЪЬтЃК
ЕФбЇЩњНјааСЫЬхжЪВтЪдЃЌВЂНЋВтЪдЪ§ОнжЦГЩШчЯТЭГМЦЭМЃЎЧыИљОнЯрЙиаХЯЂНтД№ЯТУцЕФЮЪЬтЃК
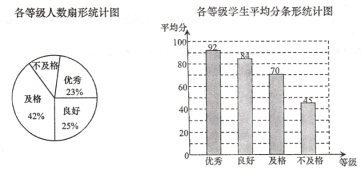
![]() ЩШаЮЭГМЦЭМжаЃЌЁАВЛМАИёЁБ ЕШМЖЫљдкЩШаЮдВаФНЧЕФЖШЪ§ЪЧЖрЩйЃП
ЩШаЮЭГМЦЭМжаЃЌЁАВЛМАИёЁБ ЕШМЖЫљдкЩШаЮдВаФНЧЕФЖШЪ§ЪЧЖрЩйЃП
![]() ЧѓВЮМгБОДЮВтЪдбЇЩњЕФЦНОљГЩМЈЃЛ
ЧѓВЮМгБОДЮВтЪдбЇЩњЕФЦНОљГЩМЈЃЛ
![]() ШєВЮМгБОДЮВтЪдЁАСМКУЁБМАЁАСМКУЁБвдЩЯЕШМЖЕФбЇЩњЙВга
ШєВЮМгБОДЮВтЪдЁАСМКУЁБМАЁАСМКУЁБвдЩЯЕШМЖЕФбЇЩњЙВга![]() ШЫЃЌЧыФуЙРМЦШЋаЃАЫФъМЖЁАВЛМАИёЁБЕШМЖЕФбЇЩњДѓдМгаЖрЩйШЫЃЎ
ШЫЃЌЧыФуЙРМЦШЋаЃАЫФъМЖЁАВЛМАИёЁБЕШМЖЕФбЇЩњДѓдМгаЖрЩйШЫЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
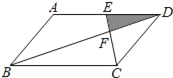
ЁОЬтФПЁПШчЭМЃЌЦНааЫФБпаЮABCDжаЃЌEЮЊADЕФжаЕуЃЌвбжЊЁїDEFЕФУцЛ§ЮЊ1ЃЌдђЦНааЫФБпаЮABCDЕФУцЛ§ЮЊ_______ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЩчЧјгЛдОЮЊЁАПЙЛїЗЮбзЁБОшПюЃЌИљОнОшПюЧщПіЃЈОшПюЪ§ЮЊе§Ъ§ЃЉжЦзївдЯТЭГМЦЭМБэЃЌЕЋЙЄзїШЫдБВЛаЁаФАбФЋЫЎЕЮдкЭГМЦБэЩЯЃЌВПЗжЪ§ОнПДВЛЧхГўЃЎ
ЃЈ1ЃЉЙВгаЖрЩйШЫОшПюЃП
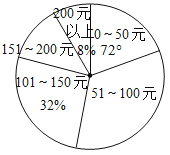
ЃЈ2ЃЉШчЙћОшПю0ЁЋ50дЊЕФШЫЪ§дкЩШаЮЭГМЦЭМжаЫљеМЕФдВаФНЧЮЊ72ЁуЃЌФЧУДОшПю51ЁЋ100дЊЕФгаЖрЩйШЫЃП
ОшПю | ШЫЪ§ |
0ЁЋ50дЊ | |
51ЁЋ100дЊ | |
101ЁЋ150дЊ | |
151ЁЋ200дЊ | 6 |
200дЊвдЩЯ | 4 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
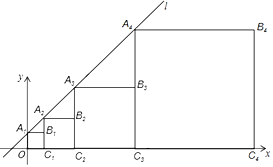
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌжБЯпlЃКyЃНx+1гыyжсНЛгкЕуA1ЃЌШчЭМЫљЪОЃЌвРДЮзїе§ЗНаЮOA1B1C1ЃЌе§ЗНаЮC1A2B2C2ЃЌе§ЗНаЮC2A3B3C3ЃЌе§ЗНаЮC3A4B4C4ЃЌЁЁЃЌЕуA1ЃЌA2ЃЌA3ЃЌA4ЃЌЁЁдкжБЯпlЩЯЃЌЕуC1ЃЌC2ЃЌC3ЃЌC4ЃЌЁЁдкxжсе§АыжсЩЯЃЌдђЧАnИіе§ЗНаЮЖдНЧЯпГЄЕФКЭЪЧ____________ЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com