
【题目】如图,Rt△ABC中,∠BCA=90°,AC=BC,点D是BC的中点,点F在线段AD上,DF=CD,BF交CA于E点,过点A作DA的垂线交CF的延长线于点G,下列结论:①CF2=EFBF;②AG=2DC;③AE=EF;④AFEC=EFEB.其中正确的结论有( )
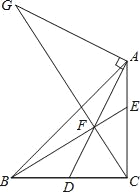
A. ①②③ B. ①②④ C. ①③④ D. ②③④
【答案】B
【解析】
根据等边对等角的性质得到∠DCF=∠DFC,继而得到DF=DB,从而得∠DBF=∠DFB,然后求出∠BFC是直角,继而得到△BCF和△CEF相似,根据相似三角形的对应边成比例,即可判断①;根据互余关系可得∠G=∠ACG,再根据等角对等边得到AG=AC,然后求出AG=BC,利用“AAS”证明△BCE和△AGF全等,根据全等三角形的性质得到AG=BC,即可判断②;根据角的互余关系求出∠EAF+∠ADC=90°,∠AFE+∠DFC=90°,再根据∠ADC的正切值为2可知∠ADC≠60°,继而得到∠EAF≠∠EFA,从而得AE≠EF,即可判断③;证明△CEF和△BCE相似,从而得EC2=EFEB,再根据全等三角形的对应边相等得到AF=CE,即可判断④,由此即可得到答案.
∵DF=CD,
∴∠DCF=∠DFC,
∵AC=BC,点D是BC的中点,
∴DF=DB=DC,
∴∠DBF=∠DFB,
又∵∠DBF+∠DFB+∠DFC+∠DCF=180°,
∴∠BFC=![]() ×180°=90°,
×180°=90°,
∴CF⊥BE,
∴Rt△BCF∽Rt△CEF,
∴![]() ,
,
∴CF2=EFBF,故①正确;
∵AG⊥AD,
∴∠G+∠AFG=90°,
又∵∠ACG+∠DCF=90°,∠DCF=∠DFC=∠AFG,
∴∠G=∠ACG,
∴AG=AC,
∵AC=BC,
∴AG=BC,
又∵∠CBE=∠ACG,
∴∠CBE=∠G,
在△BCE和△AGF中,
 ,
,
∴△BCE≌△AGF(AAS),
∴AG=BC,
∵点D是BC的中点,
∴BC=2DC,
∴AG=2DC,故②正确;
根据角的互余关系,∠EAF+∠ADC=90°,∠AFE+∠DFC=90°,
∵tan∠ADC=2,
∴∠ADC≠60°,
∵∠DCF=∠DFC,
∴∠FDC≠∠DFC,
∴∠EAF≠∠EFA,
∴AE≠EF,故③错误;
∵∠ACB=90°,CF⊥BE,
∴△CEF∽△BCE,
∴![]() ,
,
∴EC2=EFEB,
∵△BCE≌△AGF(已证),
∴AF=EC,
∴AFEC=EFEB,故④正确;
所以,正确的结论有①②④,
故选B.


科目:初中数学 来源: 题型:
【题目】下面是小董设计的“作已知圆的内接正三角形”的尺规作图过程.
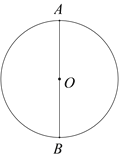
已知:⊙O.
求作:⊙O的内接正三角形.
作法:如图,
①作直径AB;
②以B为圆心,OB为半径作弧,与⊙O交于C,D两点;
③连接AC,AD,CD.
所以△ACD就是所求的三角形.
根据小董设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明:
证明:在⊙O中,连接OC,OD,BC,BD,
∵OC=OB=BC,
∴△OBC为等边三角形(_______________)(填推理的依据).
∴∠BOC=60°.
∴∠AOC=180°-∠BOC=120°.
同理∠AOD=120°,
∴∠COD=∠AOC=∠AOD=120°.
∴AC=CD=AD(_______________)(填推理的依据).
∴△ACD是等边三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC与△ADE中,∠C=∠AED=90°,点E在AB上,那么添加下列一个条件后,仍无法判定△ABC∽△DAE的是( )
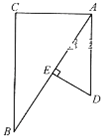
A. ![]() B. ∠B =∠D C. AD∥BC D. ∠BAC=∠D
B. ∠B =∠D C. AD∥BC D. ∠BAC=∠D
查看答案和解析>>
科目:初中数学 来源: 题型:
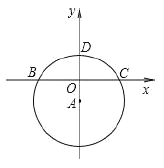
【题目】定义:如果一条直线与一条曲线有且只有一个交点,且曲线位于直线的同旁,称之为直线与曲线相切,这条直线叫做曲线的切线,直线与曲线的唯一交点叫做切点.
(1)如图,在平面直角坐标系中,点![]() 为坐标原点,以点
为坐标原点,以点![]() 为圆心,5为半径作圆
为圆心,5为半径作圆![]() ,交
,交![]() 轴的负半轴于点
轴的负半轴于点![]() ,求过点
,求过点![]() 的圆
的圆![]() 的切线的解析式;
的切线的解析式;
(2)若抛物线![]() (
(![]() )与直线
)与直线![]() (
(![]() )相切于点
)相切于点![]() ,求直线的解析式;
,求直线的解析式;
(3)若函数![]() 的图象与直线
的图象与直线![]() 相切,且当
相切,且当![]() 时,
时,![]() 的最小值为
的最小值为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)如图,△ABC内接于⊙O,AB=AC,BD为⊙O的弦,且AB∥CD,过点A作⊙O的切线AE与DC的延长线交于点E,AD与BC交于点F.

(1)求证:四边形ABCE是平行四边形;
(2)若AE=6,CD=5,求OF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知x1、x2是一元二次方程2x2-2x+m+1=0的两个实根.
(1)求实数m的取值范围;
(2)如果m满足不等式7+4x1x2>x12+x22,且m为整数.求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数的图象与x轴交于A(﹣3,0)和B(1,0)两点,交y轴于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.

(1)求二次函数的解析式;
(2)根据图象直接写出使一次函数值大于二次函数值的x的取值范围;
(3)若直线与y轴的交点为E,连结AD、AE,求△ADE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图示意图,A点的坐标为(2,2),点C在线段OA上运动(点C不与O、A重合),过点C作CD⊥x轴于D,再以CD为一边在CD右侧画正方形CDEF.连接AF并延长交x轴于B,连接OF.若△BEF与△OEF相似,则点B的坐标是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+1(k≠0)与反比例函数![]() (m≠0)的图象有公共点A(1,2).直线l⊥x轴于点N(3,0),与一次函数和反比例函数的图象分别交于点B,C.
(m≠0)的图象有公共点A(1,2).直线l⊥x轴于点N(3,0),与一次函数和反比例函数的图象分别交于点B,C.
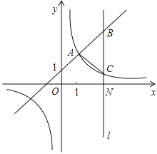
(1)求一次函数与反比例函数的解析式;
(2)求△ABC的面积?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com