
 ,
, 与
与 成正比例,
成正比例, 与
与 成反比例,且当
成反比例,且当 时,
时, ;当
;当 时,
时, .(1)求
.(1)求 与
与 的函数关系式;(2)当
的函数关系式;(2)当 时,求
时,求 的值.
的值. 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源:不详 题型:解答题
| 档次 | 第一档 | 第二档 | 第三档 |
| 每月用电量x(度) | 0<x≤140 | | |

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
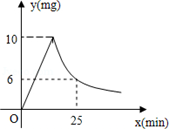
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
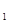 (元),节假日购票款为y
(元),节假日购票款为y (元)。y
(元)。y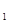 、y
、y 与x之间的函数图像如图所示
与x之间的函数图像如图所示
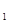 , y
, y 与x之间的函数解析式
与x之间的函数解析式查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| | A种产品 | B种产品 |
| 成本 (万元/件) | 0.6 | 0.9 |
| 利润 (万元/件) | 0.2 | 0.4 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 、
、 两座城市之间有一条高速公路,甲、乙两辆汽车同时分别从这条路两端的入口处驶入,并始终在高速公路上正常行驶.甲车驶往
两座城市之间有一条高速公路,甲、乙两辆汽车同时分别从这条路两端的入口处驶入,并始终在高速公路上正常行驶.甲车驶往 城,乙车驶往
城,乙车驶往 城,甲车在行驶过程中速度始终不变.甲车距
城,甲车在行驶过程中速度始终不变.甲车距 城高速公路入口处的距离
城高速公路入口处的距离 (千米)与行驶时间
(千米)与行驶时间 (时)之间的关系如图.
(时)之间的关系如图.
 关于
关于 的表达式;
的表达式; (千米).请直接写出
(千米).请直接写出 关于
关于 的表达式;
的表达式; (千米/时)并保持匀速行驶,结果比甲车晚40分钟到达终点,求乙车变化后的速度
(千米/时)并保持匀速行驶,结果比甲车晚40分钟到达终点,求乙车变化后的速度 .
.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com