
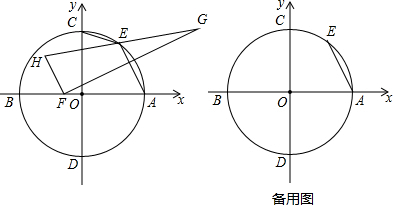
分析 (1)根据点E的坐标利用勾股定理求得圆的半径,然后利用院内接四边形的性质求得∠AEC的度数即可;
(2)连接EF,则得到EF=EG,从而得到∠EFG=∠G,然后根据∠HFG=90°,得到∠EFH=∠H,利用等角对等边得到EF=HE,从而证得HE=EG;
(3)如图,连接OE、EF,根据HG为切线得到∠GEA+∠OEA=90°,然后根据OE=OA得到∠OEA=∠EAO,再利用点G与点F关于AE对称,得到∠GEA=∠AEF,进而得到EF⊥AB,从而求得结论.
解答 解:(1)∵点E(3,4),
∴⊙O的半径为$\sqrt{{3}^{2}+{4}^{2}}$=5,
∵∠AOC=90°,
∴∠ABC=45°,
∴∠AEC=135°;
(2)如图1,连接EF,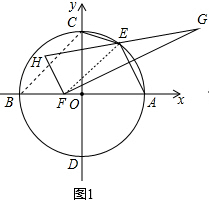
则EF=EG,
∴∠EFG=∠G,
∵∠HFG=90°,
∴∠EFH=∠H,
∴EF=HE,
∴HE=EG;
(3)如图2,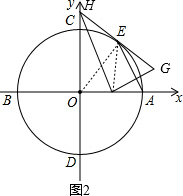
连接OE、EF,
∵HG为切线,
∴∠GEA+∠OEA=90°,
∵OE=OA,
∴∠OEA=∠EAO,
∵点G与点F关于AE对称,
∴∠GEA=∠AEF,
∴∠AEF+∠EAO=90°,
∴EF⊥AB,
∴点F的坐标为(3,0).
点评 本题考查了圆的综合题.解答该题时,用到了坐标与图形的性质、切线的判定与性质等知识点.在解答(3)题时,也用到了对称点的性质,难度较大.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
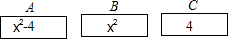 如图所示(背面完全相同)A、B、C三张卡片,正面分别写上整式x2-4,x2,4;现将这三张卡片背面向上洗匀,从中随机抽取两张,然后将所抽取卡片上的两个整式分别放在“=”的两边,组成一个等式.
如图所示(背面完全相同)A、B、C三张卡片,正面分别写上整式x2-4,x2,4;现将这三张卡片背面向上洗匀,从中随机抽取两张,然后将所抽取卡片上的两个整式分别放在“=”的两边,组成一个等式.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
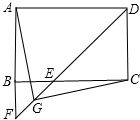 如图,在矩形ABCD中,∠ADC的平分线交BC于点E、交AB的延长线于点F,G是EF的中点,连接AG、CG.
如图,在矩形ABCD中,∠ADC的平分线交BC于点E、交AB的延长线于点F,G是EF的中点,连接AG、CG.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
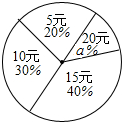 尼泊尔地震,波及西藏,人们纷纷献出爱心,某学校学生会向全校1200名学生发起了爱心捐款活动,为了解捐款情况,随机抽查了部分学生的捐款金额,王老师把所得的数据绘制成如图统计图和统计表,请根据相关信息,解答下列问题:
尼泊尔地震,波及西藏,人们纷纷献出爱心,某学校学生会向全校1200名学生发起了爱心捐款活动,为了解捐款情况,随机抽查了部分学生的捐款金额,王老师把所得的数据绘制成如图统计图和统计表,请根据相关信息,解答下列问题:| 金额(元) | 5 | 10 | 15 | 20 |
| 人数 | 10 | 15 | 20 | b |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 “龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场.图中的图象刻画了“龟兔再次赛跑”的故事(x表示乌龟从起点出发所行的时间,y1表示乌龟所行的路程,y2表示兔子所行的路程).请你根据图象回答下列问题.
“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场.图中的图象刻画了“龟兔再次赛跑”的故事(x表示乌龟从起点出发所行的时间,y1表示乌龟所行的路程,y2表示兔子所行的路程).请你根据图象回答下列问题.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com