
 ,15不小心被墨汁涂抹了一个,只记得这组数的中位数与平均数相等,那么这组数据的中位数是20或17.5.
,15不小心被墨汁涂抹了一个,只记得这组数的中位数与平均数相等,那么这组数据的中位数是20或17.5. 分析 因为中位数的值与大小排列顺序有关,而此题中x的大小位置未定,故应该分类讨论x所处的所有位置情况:从小到大(或从大到小)排列在中间(在第二位或第三位结果不影响);结尾;开始的位置.
解答 解:(1)将这组数据从大到小的顺序排列后20,20,x,15,处于中间位置的那个数是20,x,
那么由中位数的定义可知,(20+x)÷2=(20+20+x+15)÷4,
x=-$\frac{25}{3}$,不符合题意;
(2)将这组数据从大到小的顺序排列后20,20,15,x,中位数是(20+15)÷2=17.5,
此时平均数是(20+20+x+15)÷4=17.5,
x=15,符合题意;
(3)将这组数据从大到小的顺序排列后x,20,20,15,中位数是20,
平均数(20+20+x+15)÷4=20,
x=25,符合中位数定义;
所以中位数是20或17.5.
故答案为:20或17.5.
点评 本题结合平均数考查了确定一组数据的中位数的能力.涉及到分类讨论思想,较难,要明确中位数的值与大小排列顺序有关,一些学生往往对这个概念掌握不清楚,计算方法不明确而解答不完整.注意找中位数的时候一定要先排好顺序,然后再根据奇数和偶数个来确定中位数,如果数据有奇数个,则正中间的数字即为所求.如果是偶数个则找中间两位数的平均数.


 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
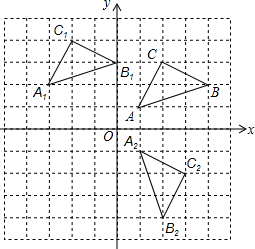 如图,方格纸中的每个小方格都是边长为1的单位小正方形,每个小正方形的顶点称为格点,△ABC的顶点都在格点上,建立平面直角坐标系后,点A、B、C的坐标分别为(1,1),(4,2),(2,3)
如图,方格纸中的每个小方格都是边长为1的单位小正方形,每个小正方形的顶点称为格点,△ABC的顶点都在格点上,建立平面直角坐标系后,点A、B、C的坐标分别为(1,1),(4,2),(2,3)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图:在△ABC中,AB=AC,P是BC上一点,PE⊥AB于E,PF⊥AC于F,CG⊥AB于G.
已知:如图:在△ABC中,AB=AC,P是BC上一点,PE⊥AB于E,PF⊥AC于F,CG⊥AB于G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com