
分析 (1)设有x名工人加工G型装置,则有(80-x)名工人加工H型装置,利用每台GH型产品由4个G型装置和3个H型装置配套组成得出等式求出答案;
(2)设招聘a名新工人加工G型装置,设x名工人加工G型装置,(80-x)名工人加工H型装置,进而利用每天加工的G、H型装置数量正好全部配套组成GH型产品得出等式表示出x的值,进而利用不等式解法得出答案.
解答 解:(1)设有x名工人加工G型装置,
则有(80-x)名工人加工H型装置,
根据题意,$\frac{6x}{4}$=$\frac{3(80-x)}{3}$,
解得x=32,
则80-32=48(套),
答:每天能组装48套GH型电子产品;
(2)设招聘a名新工人加工G型装置
仍设x名工人加工G型装置,(80-x)名工人加工H型装置,
根据题意,$\frac{6x+4a}{4}$=$\frac{3(80-x)}{3}$,
整理可得,x=$\frac{160-2a}{5}$,
另外,注意到80-x≥$\frac{1200}{20}$,即x≤20,
于是$\frac{160-2a}{5}$≤20,
解得:a≥30,
答:至少应招聘30名新工人,
点评 此题主要考查了一元一次方程的应用以及一元一次不等式的应用,根据题意正确得出等量关系是解题关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1<y2 | B. | y1>y2 | C. | y1=y2 | D. | 以上都不对 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
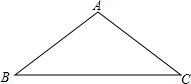 如图,在△ABC中,AB=AC=10,BC=16.
如图,在△ABC中,AB=AC=10,BC=16.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (a2)3=a5 | B. | 3$\sqrt{5}-\sqrt{5}$=3 | C. | $\root{3}{-27}$=-3 | D. | (a-b)2=a2-b2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com