
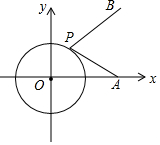
 如图,在平面直角坐标系中,点A(4,0),B(4,4),点P在半径为2的圆O上运动,则$\frac{1}{2}$AP+BP的最小值是5.
如图,在平面直角坐标系中,点A(4,0),B(4,4),点P在半径为2的圆O上运动,则$\frac{1}{2}$AP+BP的最小值是5. 分析 如图,取点K(1,0),连接OP、PK、BK.由△POK∽△AOP,可得$\frac{PK}{PA}$=$\frac{OP}{OA}$=$\frac{1}{2}$,推出PK=$\frac{1}{2}$PA,在△PBK中,PB+PK≥BK,推出PB+$\frac{1}{2}$PA=PB+PK的最小值为BK的长.
解答 解:如图,取点K(1,0),连接OP、PK、BK.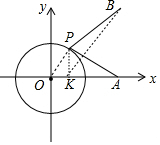
∵OP=2,OA=4,OK=1,
∴$\frac{OP}{OA}$=$\frac{OK}{OP}$=$\frac{1}{2}$,∵∠POK=∠AOP,
∴△POK∽△AOP,
∴$\frac{PK}{PA}$=$\frac{OP}{OA}$=$\frac{1}{2}$,
∴PK=$\frac{1}{2}$PA,
∴PB+$\frac{1}{2}$PA=PB+PK,
在△PBK中,PB+PK≥BK,
∴PB+$\frac{1}{2}$PA=PB+PK的最小值为BK的长,
∵B(4,4),K(1,0),
∴BK=$\sqrt{{3}^{2}+{4}^{2}}$=5.
故答案为5.
点评 本题考查坐标与图形的性质、相似三角形的判定和性质、三角形的三边关系、两点之间的距离公式等知识,解题的关键是灵活运用所学知识解决问题,学会用转化的思想思考问题,属于中考填空题中的压轴题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
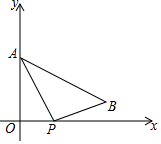 如图,在平面直角坐标系中,点A(0,3)、点B(4,1),点P是x轴正半轴上一动点.给出4个结论:
如图,在平面直角坐标系中,点A(0,3)、点B(4,1),点P是x轴正半轴上一动点.给出4个结论:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 已知,正六边形ABCDEF在直角坐标系内的位置如图所示,点A的坐标为A(-1,0),点B在原点,把正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转,每次翻转60°,经过2016次翻转之后,点B的经过的路径长是(2016$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$).
已知,正六边形ABCDEF在直角坐标系内的位置如图所示,点A的坐标为A(-1,0),点B在原点,把正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转,每次翻转60°,经过2016次翻转之后,点B的经过的路径长是(2016$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
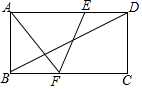 如图,在矩形ABCD中,点E、F分别是AD、BC上的点,连接AF、EF,EF与对角线BD交于点O.若AE=AF=CF=12,∠AEF=2∠ADB,则矩形ABCD的面积为108$\sqrt{3}$.
如图,在矩形ABCD中,点E、F分别是AD、BC上的点,连接AF、EF,EF与对角线BD交于点O.若AE=AF=CF=12,∠AEF=2∠ADB,则矩形ABCD的面积为108$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
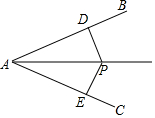 如图,点P在∠BAC的角平分线上,PD⊥AB,PE⊥AC,垂足分别为D、E,则△APD与△APE全等的理由是( )
如图,点P在∠BAC的角平分线上,PD⊥AB,PE⊥AC,垂足分别为D、E,则△APD与△APE全等的理由是( )| A. | SAS | B. | AAS | C. | SSS | D. | HL |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
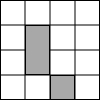 如图是4×4正方形网格,其中已有3个小方格涂成了黑色.现在要从其余13个白色小方格中选出一个也涂成黑色的图形成为轴对称图形,这样的白色小正方格有( )
如图是4×4正方形网格,其中已有3个小方格涂成了黑色.现在要从其余13个白色小方格中选出一个也涂成黑色的图形成为轴对称图形,这样的白色小正方格有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com