
| ЗНГЬ | x1 | x2 | x1+x2 | x1•x2 |
| x2-5x+6=0 | 2 | 3 | 5 | 6 |
| 2x2-3x+1=0 | $\frac{1}{2}$ | 1 | $\frac{3}{2}$ | $\frac{1}{2}$ |
| 5x2-7x+2=0 | $\frac{2}{5}$ | 1 | $\frac{7}{5}$ | $\frac{2}{5}$ |
ЗжЮі ЪзЯШЧѓЕУЗНГЬЕФИљЃЌНјвЛВНМЦЫуСНИљЕФКЭгыСНИљЕФЛ§ЃЌЙщФЩЕУГіИљгыЯЕЪ§ЕФЙиЯЕx1+x2=-$\frac{b}{a}$ЃЌx1x2=$\frac{c}{a}$ЃЎ
НтД№ НтЃКЬюБэШчЯТЃК
| ЗНГЬ | x1 | x2 | x1+x2 | x1•x2 |
| x2-5x+6=0 | 2 | 3 | 5 | 6 |
| 2x2-3x+1=0 | $\frac{1}{2}$ | 1 | $\frac{3}{2}$ | $\frac{1}{2}$ |
| 5x2-7x+2=0 | $\frac{2}{5}$ | 1 | $\frac{7}{5}$ | $\frac{2}{5}$ |
ЕуЦР БОЬтПМВщСЫИљгыЯЕЪ§ЕФЙиЯЕЃКШєx1ЃЌx2ЪЧвЛдЊЖўДЮЗНГЬax2+bx+c=0ЃЈaЁй0ЃЉЕФСНИљЪБЃЌx1+x2=-$\frac{b}{a}$ЃЌx1x2=$\frac{c}{a}$ЃЎ


 вЛЯпУћЪІЬсгХЪдОэЯЕСаД№АИ
вЛЯпУћЪІЬсгХЪдОэЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
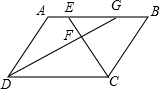 ШчЭМЃК?ABCDжаЃЌЁЯІЂCDЕФЦНЗжЯпCEНЛБпADгкEЃЌЁЯABCЕФЦНЗжЯпBGНЛCEгкFЃЌНЛADгкGЃЌЧѓжЄЃКAE=BGЃЎ
ШчЭМЃК?ABCDжаЃЌЁЯІЂCDЕФЦНЗжЯпCEНЛБпADгкEЃЌЁЯABCЕФЦНЗжЯпBGНЛCEгкFЃЌНЛADгкGЃЌЧѓжЄЃКAE=BGЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
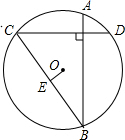 ШчЭМЫљЪОЃЌвбжЊЁбOЯвABЁЭCDЃЌOEЁЭBCгкЕуEЃЌЧѓжЄЃКAD=2OEЃЎ
ШчЭМЫљЪОЃЌвбжЊЁбOЯвABЁЭCDЃЌOEЁЭBCгкЕуEЃЌЧѓжЄЃКAD=2OEЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com