
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 射击次数(n) | 8 | 15 | 20 | 30 | 40 | 50 |
| 击中靶心频数(m) | 6 | 12 | 17 | 24 | 32 | 40 |
| 击中靶心频率($\frac{m}{n}$) | 0.75 | 0.80 | 0.85 | 0.80 | 0.80 | 0.80 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 方程x2-x+1=0的两实数根之和等于-1 | |
| B. | 方程x2+x+1=0的两实数根之积等于1 | |
| C. | 方程x2-x-1=0的两实数根之和等于1 | |
| D. | 方程x2+x-1=0的两实数根之积等于1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
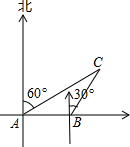 如图所示,某船以每小时40海里的速度向正东方向航行,在点A测得岛C在北偏东60°方向上,航行半小时后到达点B,测得该岛C在北偏东30方向上,已知该岛周围18海里内有暗礁.
如图所示,某船以每小时40海里的速度向正东方向航行,在点A测得岛C在北偏东60°方向上,航行半小时后到达点B,测得该岛C在北偏东30方向上,已知该岛周围18海里内有暗礁.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com