
【题目】如图,在平面直角坐标中,抛物线y=ax2+bx+c过点A(﹣1,0),B(3,0),C(0,3),点P是直线BC上方抛物线上的一动点,PE∥y轴,交直线BC于点E连接AP,交直线BC于点 D.
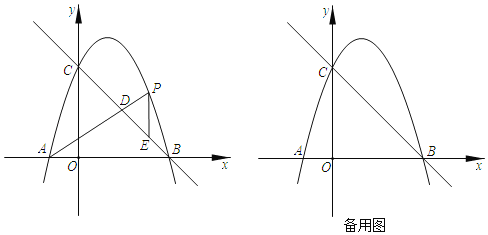
(1)求抛物线的函数表达式;
(2)当AD=2PD时,求点P的坐标;
(3)求线段![]() 的最大值;
的最大值;
(4)当线段![]() 最大时,若点F在直线BC上且∠EFP=2∠ACO,直接写出点F的坐标.
最大时,若点F在直线BC上且∠EFP=2∠ACO,直接写出点F的坐标.
【答案】(1)y=﹣x2+2x+3;(2)P(1,4)或P(2,3);(3)当t=2时,![]() 的值最大为4;(4)
的值最大为4;(4)![]()
【解析】
(1)由于抛物线与x轴的两个交点坐标已知,可把抛物线的解析式设成交点式,再代入另一已知点坐标便可求出解析式;
(2)过A作EF⊥x轴,与BC相交于点F,用待定系数法求出BC的解析式,设P点的横坐标为t,进而求得AF与PE,由相似三角形的比例线段求得t便可;
(3)根据PE关于t的函数解析式,由函数的性质求出其最大值便可;
(4)分两种情况:①当F点在PE的左边时,过点P作PM⊥BC于点M,过E作EN⊥x轴于点N,过点F作FQ⊥x轴于点Q,过点O作OG⊥AC于点G,取AC的中点H,连接OH,通过三角形相似求出MF的值便可;②将求得的F点坐标,关于PM对称点便是另一F点.
(1)设抛物线的解析式为:y=a(x+1)(x-3)(a≠0),
把C(0,3)代入得,3=a×1×(-3),
∴a=-1,
∴抛物线的解析式为:y=-(x+1)(x-3),即y=-x2+2x+3;
(2)过A作AF⊥x轴,与BC相交于点F,如图1,设P(t,﹣t2+2t+3),
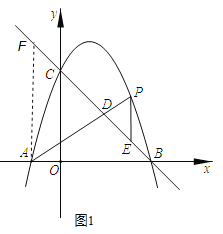
则AF∥PE,
设BC的解析式为y=kx+b(k≠0),则![]() ,
,
解得,![]() ,
,
∴直线BC的解析式为:y=﹣x+3,
∴E(t,﹣t+3),F(﹣1,4),
∴AF=4,PE=﹣t2+3t,
∵AF∥PE,
∴△AFD∽△PED,
∴![]() ,
,
∵AD=2PD,
∴![]() ,解得,t=1或2,
,解得,t=1或2,
∴P(1,4)或P(2,3);
(3)∵PE的解析式为:PE=﹣t2+3t
过点E作EH⊥y轴,如图2
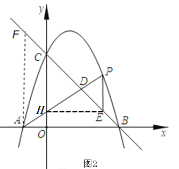
∴![]()
∴![]()
∴当t=2时,![]() 的值最大为4;
的值最大为4;
(4)①当F点在
过点P作PM⊥BC于点M,过E作EN⊥x轴于点N,过点F作FQ⊥x轴于点Q,过点O作OG⊥AC于点G,取AC的中点H,连接OH,如图3,

由(3)知,当![]() 取最大值时,P(2,3),PE=2,E(2,1),
取最大值时,P(2,3),PE=2,E(2,1),
∵OB=OC=3,
∴∠OBC=∠OCB=45°,
∴BE=![]() ,∠PEM=45°,
,∠PEM=45°,
∴PM=EM=![]() ,
,
∵![]() ,
,
∴![]() ,
,
![]() ,
,
∴![]() ,∠OHG=2∠ACO,
,∠OHG=2∠ACO,
∵∠EFP=2∠ACO,
∴∠EFP=∠OHG,
∵∠OGH=∠PMF,
∴△OGH∽△PMF,
∴![]() ,即
,即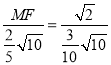 ,
,
∴MF=![]() ,
,
∴BF=BE+EM+MF=![]() ,
,
∴FQ=BQ=![]() ,
,
∴OQ=BQ-BO=![]() ,
,
∴F(![]() ,
,![]() ),
),
②当F点在PE的右边时,此时的F点恰好与(![]() ,
,![]() )关于PM对称,易求此时F(
)关于PM对称,易求此时F(![]() ,
,![]() ).
).
故F的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
【题目】为实现区域教育均衡发展,我市计划对某县![]() 、
、![]() 两类薄弱学校全部进行改造.根据预算,共需资金1575万元.改造一所
两类薄弱学校全部进行改造.根据预算,共需资金1575万元.改造一所![]() 类学校和两所
类学校和两所![]() 类学校共需资金230万元;改造两所
类学校共需资金230万元;改造两所![]() 类学校和一所
类学校和一所![]() 类学校共需资金205万元.
类学校共需资金205万元.
(1)改造一所![]() 类学校和一所
类学校和一所![]() 类学校所需的资金分别是多少万元?
类学校所需的资金分别是多少万元?
(2)若该县的![]() 类学校不超过5所,则
类学校不超过5所,则![]() 类学校至少有多少所?
类学校至少有多少所?
(3)我市计划今年对该县![]() 、
、![]() 两类学校共6所进行改造,改造资金由国家财政和地方财政共同承担.若今年国家财政拨付的改造资金不超过400万元;地方财政投入的改造资金不少于70万元,其中地方财政投入到
两类学校共6所进行改造,改造资金由国家财政和地方财政共同承担.若今年国家财政拨付的改造资金不超过400万元;地方财政投入的改造资金不少于70万元,其中地方财政投入到![]() 、
、![]() 两类学校的改造资金分别为每所10万元和15万元.请你通过计算求出有几种改造方案?
两类学校的改造资金分别为每所10万元和15万元.请你通过计算求出有几种改造方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
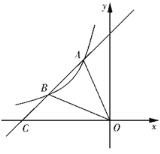
【题目】如图,直线![]() 与反比例函数
与反比例函数![]() 的图像交点A.点B,与x轴相交于点C,其中点A的坐标为(-2,4),点B的纵坐标为2.
的图像交点A.点B,与x轴相交于点C,其中点A的坐标为(-2,4),点B的纵坐标为2.
(1)当x为何值时,一次函数的值大于反比例函数的值.(直接写出来)
(2)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
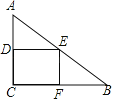
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,矩形CDEF的顶点E在边AB上,D,F两点分别在边AC,BC上,且![]() ,将矩形CDEF以每秒1个单位长度的速度沿射线CB方向匀速运动,当点C与点B重合时停止运动,设运动时间为t秒,矩形CDEF与△ABC重叠部分的面积为S,则反映S与t的函数关系的图象为( )
,将矩形CDEF以每秒1个单位长度的速度沿射线CB方向匀速运动,当点C与点B重合时停止运动,设运动时间为t秒,矩形CDEF与△ABC重叠部分的面积为S,则反映S与t的函数关系的图象为( )
A.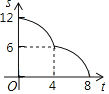 B.
B.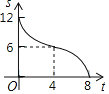 C.
C.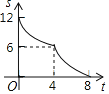 D.
D.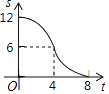
查看答案和解析>>
科目:初中数学 来源: 题型:
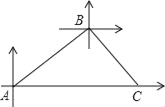
【题目】甲、乙两条轮船同时从港口A出发,甲轮船以每小时30海里的速度沿着北偏东60°的方向航行,乙轮船以每小时15海里的速度沿着正东方向行进,1小时后,甲船接到命令要与乙船会合,于是甲船改变了行进的速度,沿着东南方向航行,结果在小岛C处与乙船相遇.假设乙船的速度和航向保持不变,求:
(1)港口A与小岛C之间的距离;
(2)甲轮船后来的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
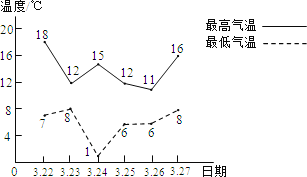
【题目】如图所示为3月22日至27日间,我区每日最高气温与最低气温的变化情况.
(1)最低气温的中位数是 ℃;3月24日的温差是 ℃;
(2)分别求出3月22日至27日间的最高气温的平均数、最低气温的平均数;
(3)经过计算,最高气温和最低气温的方差分别为6.33、5.67,数据更稳定的是最高气温还是最低气温?
查看答案和解析>>
科目:初中数学 来源: 题型:
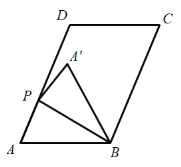
【题目】如图,在平行四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是射线
是射线![]() 上一点,连接
上一点,连接![]() ,沿
,沿![]() 将三角形
将三角形![]() 折叠,得三角形
折叠,得三角形![]() .
.
(1)当![]() 时,
时,![]() =_______度;
=_______度;
(2)如图,当![]() 时,求线段
时,求线段![]() 的长度;
的长度;

(3)当点![]() 落在平行四边形
落在平行四边形![]() 的边上时,直接写出线段
的边上时,直接写出线段![]() 的长度.
的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com