
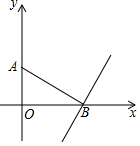
 如图,点A(0,3),B(6,0),过点B作AB的垂线l.若直线l上存在点C,满足BC=2$\sqrt{5}$,则点C的坐标为(8,4)或(4,-4).
如图,点A(0,3),B(6,0),过点B作AB的垂线l.若直线l上存在点C,满足BC=2$\sqrt{5}$,则点C的坐标为(8,4)或(4,-4). 分析 先利用待定系数法求出直线AB的解析式为y=-$\frac{1}{2}$x+3,再根据互相垂直的两直线斜率之积为-1可设直线l的解析式为y=2x+b,将B(6,0)代入,求出直线l的解析式为y=2x-12.设点C的坐标为(x,2x-12).根据BC=2$\sqrt{5}$,列出方程(x-6)2+(2x-12)2=20,解方程即可.
解答 解:∵点A(0,3),B(6,0),
∴直线AB的解析式为y=-$\frac{1}{2}$x+3,
∵l⊥AB,
∴可设直线l的解析式为y=2x+b,
将B(6,0)代入,得12+b=0,解得b=-12,
即直线l的解析式为y=2x-12.
设点C的坐标为(x,2x-12).
∵BC=2$\sqrt{5}$,
∴(x-6)2+(2x-12)2=20,
整理,得x2-12x+32=0,
解得x=8或4,
∴点C的坐标为(8,4)或(4,-4).
故答案为(8,4)或(4,-4).
点评 本题考查了待定系数法求一次函数的解析式,互相垂直的两直线斜率之积为-1,一次函数图象上点的坐标特征,两点间的距离公式,求出直线l的解析式是解题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知抛物线y=-x2+bx+c与x轴交于点A和点B(3,0),与y轴交于点C(0,3),P是线段BC上一点,过点P作PN∥y轴交x轴于点N,交抛物线于点M.
已知抛物线y=-x2+bx+c与x轴交于点A和点B(3,0),与y轴交于点C(0,3),P是线段BC上一点,过点P作PN∥y轴交x轴于点N,交抛物线于点M.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,平面直角坐标系中,已知直线y=x上一点P(1,1),C为y轴上一点,连接PC,线段PC绕点P顺时针旋转90°至线段PD,过点D作直线AB⊥x轴,垂足为B,直线AB与直线y=x交于点A,且BD=3AD,连接CD,直线CD与直线y=x交于点Q,则点Q的坐标为($\frac{32}{15}$,$\frac{32}{15}$).
如图,平面直角坐标系中,已知直线y=x上一点P(1,1),C为y轴上一点,连接PC,线段PC绕点P顺时针旋转90°至线段PD,过点D作直线AB⊥x轴,垂足为B,直线AB与直线y=x交于点A,且BD=3AD,连接CD,直线CD与直线y=x交于点Q,则点Q的坐标为($\frac{32}{15}$,$\frac{32}{15}$).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 2017年 月 农历丙申(猴)年辛丑月 建国68年 | ||||||
| 日 | 一 | 二 | 三 | 四 | 五 | 六 |
| 1 初五 | 2 初六 | 3 立夏初七 | 4 初八 | |||
| a | d | |||||
| b | c | |||||
| A. | 3个 | B. | 2个 | C. | 1个 | D. | 0个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
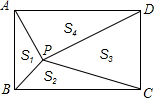 如图,点P是矩形ABCD内一点,连接PA、PB、PC、PD,已知AB=3,BC=4,设△PAB、△PBC、△PCD、△PDA的面积分别为S1、S2、S3、S4,以下判断:
如图,点P是矩形ABCD内一点,连接PA、PB、PC、PD,已知AB=3,BC=4,设△PAB、△PBC、△PCD、△PDA的面积分别为S1、S2、S3、S4,以下判断:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com