
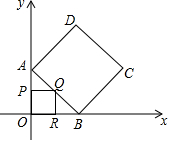
 如图,在直角坐标系中,已知A(0,4)、B(4,0),以AB为边在第一象限内作正方形ABCD,在三角形AOB内部做正方形OPQR,使P、R、Q三点分别在线段OA、OB、AB上,将正方形OPQR绕点O顺时针旋转时,求点C到点Q距离的最大值与最小值.
如图,在直角坐标系中,已知A(0,4)、B(4,0),以AB为边在第一象限内作正方形ABCD,在三角形AOB内部做正方形OPQR,使P、R、Q三点分别在线段OA、OB、AB上,将正方形OPQR绕点O顺时针旋转时,求点C到点Q距离的最大值与最小值. 分析 作CH⊥x轴于H,如图,易得△AOB为等腰直角三角形,则AB=$\sqrt{2}$OA=4$\sqrt{2}$,再利用四边形形OPQR为正方形得到OR=BR=QR=2,所以OQ=$\sqrt{2}$OR=2$\sqrt{2}$,接着利用△BHC为等腰直角三角形得到CH=BH=$\frac{\sqrt{2}}{2}$BC=4,利用勾股定理计算出OC=4$\sqrt{5}$,连接OQ、CQ,如图,利用两点之间线段最短,当点Q在线段OC上时,CQ最短,此时CQ=OC-OQ;当点Q在线段OC的反向延长线上时,CQ最长,此时CQ=OC+OQ,从而得到点C到点Q距离的最大值与最小值.
解答 解:作CH⊥x轴于H,如图,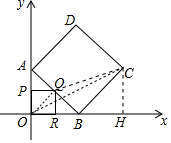
∵A(0,4)、B(4,0),
∴OA=OB=4,
∴△AOB为等腰直角三角形,AB=$\sqrt{2}$OA=4$\sqrt{2}$,
∵四边形形OPQR为正方形,
∴OR=BR=QR=2,
∴OQ=$\sqrt{2}$OR=2$\sqrt{2}$,
易得△BHC为等腰直角三角形,
而四边形形ABCD为正方形,
∴BC=AB=4$\sqrt{2}$,
∴CH=BH=$\frac{\sqrt{2}}{2}$BC=4,
在Rt△OCH中,OC=$\sqrt{{4}^{2}+{8}^{2}}$=4$\sqrt{5}$,
连接OQ、CQ,如图,
当点Q在线段OC上时,CQ最短,此时CQ=OC-OQ=4$\sqrt{5}$-2$\sqrt{2}$;
当点Q在线段OC的反向延长线上时,CQ最长,此时CQ=OC+OQ=4$\sqrt{5}$+2$\sqrt{2}$,
即点C到点Q距离的最大值为4$\sqrt{5}$+2$\sqrt{2}$,最小值为4$\sqrt{5}$-2$\sqrt{2}$.
点评 本题考查了作图-旋转变换:利用旋转的性质画图或进行几何计算.也考查了正方形的性质.


科目:初中数学 来源: 题型:解答题
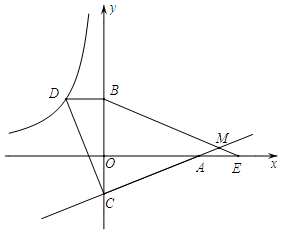 如图,已知点D在反比例函数y=$\frac{m}{x}$的图象上,过点D作x轴的平行线交y轴于点B(0,3).过点A(5,0)的直线y=kx+b与y轴于点C,且BD=OC,tan∠OAC=$\frac{2}{5}$.
如图,已知点D在反比例函数y=$\frac{m}{x}$的图象上,过点D作x轴的平行线交y轴于点B(0,3).过点A(5,0)的直线y=kx+b与y轴于点C,且BD=OC,tan∠OAC=$\frac{2}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com