
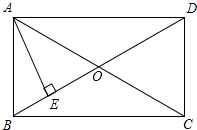
 如图,在矩形ABCD中,AD=6,对角线AC与BD相交于点O,AE⊥BD,垂足为E,ED=3BE,则AE的长为3.
如图,在矩形ABCD中,AD=6,对角线AC与BD相交于点O,AE⊥BD,垂足为E,ED=3BE,则AE的长为3. 分析 由在矩形ABCD中,AE⊥BD于E,BE:ED=1:3,易证得△OAB是等边三角形,继而求得∠BAE的度数,由△OAB是等边三角形,求出∠ADE的度数,又由AD=6,即可求得AE的长.
解答 解:∵四边形ABCD是矩形,
∴OB=OD,OA=OC,AC=BD,
∴OA=OB,
∵BE:ED=1:3,
∴BE:OB=1:2,
∵AE⊥BD,
∴AB=OA,
∴OA=AB=OB,
即△OAB是等边三角形,
∴∠ABD=60°,
∴∠ADE=90°-∠ABD=30°,
∵AE⊥BD,AD=6,
∴AE=$\frac{1}{2}$AD=3,
故答案为:3.
点评 此题考查了矩形的性质、等边三角形的判定与性质以及含30°角的直角三角形的性质.此题难度不大,注意掌握数形结合思想的应用.


 优百分课时互动系列答案
优百分课时互动系列答案科目:初中数学 来源: 题型:选择题
| A. | y=$\frac{1-x}{\sqrt{3x-1}}$ | B. | y=$\sqrt{\frac{1-x}{3x-1}}$ | C. | y=$\frac{\sqrt{3x-1}}{1-x}$ | D. | y=$\frac{1}{\sqrt{1-x}}$-$\sqrt{3x-1}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
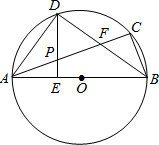 如图,?ABC是⊙O的内接三角形,AB为直径,∠CBA的平分线交AC于点F,交⊙O于点D,DE⊥AB于点E,且交AC于点P,连接AD.
如图,?ABC是⊙O的内接三角形,AB为直径,∠CBA的平分线交AC于点F,交⊙O于点D,DE⊥AB于点E,且交AC于点P,连接AD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC的外角∠DAC的平分线交BC边的垂直平分线于P点,PD⊥AB于D,PE⊥AC于E.
如图,△ABC的外角∠DAC的平分线交BC边的垂直平分线于P点,PD⊥AB于D,PE⊥AC于E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 九年级学生小明的家乡有用平直的公路连接起来的小山和明山,如图所示,小明在A处测得小山和明山的顶峰仰角均为45°.他又从A处沿公路向明山前进100m到达B处,测得小山和明山的仰角分别为30°和60°,求小山和明山的高度.(计算结果精确到1m,$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
九年级学生小明的家乡有用平直的公路连接起来的小山和明山,如图所示,小明在A处测得小山和明山的顶峰仰角均为45°.他又从A处沿公路向明山前进100m到达B处,测得小山和明山的仰角分别为30°和60°,求小山和明山的高度.(计算结果精确到1m,$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com