
【题目】甲、乙两位射击运动员参加射击训练,各射击20次,成绩如下表所示:
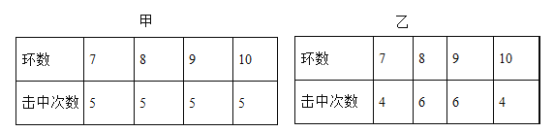
设甲、乙两位运动员射击成绩的方差分别为S 2甲和S 2乙,则下列说法正确的是
A. S 2甲<S 2乙B. S 2甲=S 2乙
C. S 2甲>S 2乙D. 无法比较S 2甲和S 2乙的大小
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,A(0,5),直线x=-5与x轴交于点D,直线y=-![]() x-
x-![]() 与x轴及直线x=-5分别交于点C,E.点B,E关于x轴对称,连接AB.
与x轴及直线x=-5分别交于点C,E.点B,E关于x轴对称,连接AB.
(1)求点C,E的坐标及直线AB的解析式;
(2)若S=S△CDE+S四边形ABDO,求S的值;
(3)在求(2)中S时,嘉琪有个想法:“将△CDE沿x轴翻折到△CDB的位置,而△CDB与四边形ABDO拼接后可看成△AOC,这样求S便转化为直接求△AOC的面积,如此不更快捷吗?”但大家经反复验算,发现S△AOC≠S,请通过计算解释他的想法错在哪里.

查看答案和解析>>
科目:初中数学 来源: 题型:
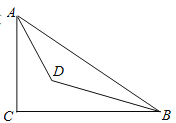
【题目】如图,在Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,AD和BD分别是∠BAC和∠ABC的平分线,它们相交于点D,则点D到BC的距离是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:在平面内,我们把既有大小又有方向的量叫做平面向量。平面向量可以用有向线段表示,有向线段的长度表示向量的大小,有向线段的方向表示向量的方向。其中大小相等,方向相同的向量叫做相等向量。如以正方形![]() 的四个顶点中某一点为起点,另一个顶点为终点作向量,可以作出8个不同的向量:
的四个顶点中某一点为起点,另一个顶点为终点作向量,可以作出8个不同的向量:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() (由于
(由于![]() 和
和![]() 是相等向量,因此只算一个)
是相等向量,因此只算一个)
⑴作两个相邻的正方形(如图一)。以其中的一个顶点为起点,另一个顶点为终点作向量,可以作出不同向量的个数记为![]() ,试求
,试求![]() 的值;
的值;
⑵作![]() 个相邻的正方形(如图二)“一字型”排开。以其中的一个顶点为起点,另一个顶点为终点作向量,可以作出不同向量的个数记为
个相邻的正方形(如图二)“一字型”排开。以其中的一个顶点为起点,另一个顶点为终点作向量,可以作出不同向量的个数记为![]() ,试求
,试求![]() 的值;
的值;
⑶作![]() 个相邻的正方形(如图三)排开。以其中的一个顶点为起点,另一个顶点为终点作向量,可以作出不同向量的个数记为
个相邻的正方形(如图三)排开。以其中的一个顶点为起点,另一个顶点为终点作向量,可以作出不同向量的个数记为![]() ,试求
,试求![]() 的值;
的值;
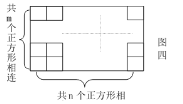
⑷作![]() 个相邻的正方形(如图四)排开。以其中的一个顶点为起点,另一个顶点为终点作向量,可以作出不同向量的个数记为
个相邻的正方形(如图四)排开。以其中的一个顶点为起点,另一个顶点为终点作向量,可以作出不同向量的个数记为![]() ,试求
,试求![]() 的值。
的值。
![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A在∠MON的边ON上,AB⊥OM于B,AE=OB,DE⊥ON于E,AD=AO,DC⊥OM于C.
(1)求证:四边形ABCD是矩形;
(2)若DE=3,OE=9,求AB、AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】苏科版九年级下册数学课本91页有这样一道习题:


(1)复习时,小明与小亮、数学老师交流了自己的两个见解,并得到了老师的认可:
①可以假定正方形的边长AB=4a,则AE=DE=2a,DF=a,利用“两边分别成比例且夹角相等的两个三角形相似”可以证明△ABE∽△DEF;请结合提示写出证明过程.
②图中的相似三角形共三对,而且可以借助于△ABE与△DEF中的比例线段来证明△EBF与它们相似.证明过程如下:

(2)交流之后,小亮尝试对问题进行了变化,在老师的帮助下,提出了新的问题,请你解答:
已知:如图,在矩形ABCD中,E为AD的中点,EF⊥EC交AB于F,连结FC.
(AB>AE)

①求证:△AEF∽△ECF;
②设BC=2,AB=a,是否存在a值,使得△AEF与△BFC相似.若存在,请求出a的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
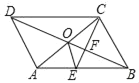
【题目】如图,ABCD的对角线AC,BD交于点O,CE平分∠BCD交AB于点E,交BD于点F,且∠ABC=60°,AB=2BC,连接OE.下列结论:①∠ACD=30°;②SABCD=ACBC;③OE:AC=![]() :6; ④SOEF=
:6; ④SOEF=![]() SABCD,成立的是_____.
SABCD,成立的是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
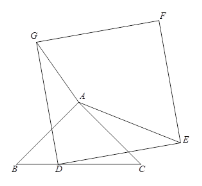
【题目】如图,已知△ABC中,∠BAC=90°,AB=AC=6.D为BC边一点,且BD∶DC=1∶2,以D为一个顶点作正方形DEFG,且DE=BC,连接AE,将正方形DEFG绕点D旋转一周,在整个旋转过程中,当AE取得最大值时AG的长为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com