
【题目】对于平面内的∠M和∠N,若存在一个常数k>0,使得∠M+k∠N=360°,则称∠N为∠M的k系补周角.如若∠M=90°,∠N=45°,则∠N为∠M的6系补周角.


(1)若∠H=120°,则∠H的4系补周角的度数为 ;
(2)在平面内AB∥CD,点E是平面内一点,连接BE,DE.
①如图1,∠D=60°,若∠B是∠E的3系补周角,求∠B的度数;
②如图2,∠ABE和∠CDE均为钝角,点F在点E的右侧,且满足∠ABF=n∠ABE,∠CDF=n∠CDE(其中n为常数且n>1),点P是∠ABE角平分线BG上的一个动点,在P点运动过程中,请你确定一个点P的位置,使得∠BPD是∠F的k系补周角,并直接写出此时的k值(用含n的式子表示).
【答案】(1)60°;(2)①75°,②当BG上的动点P为∠CDG的角平分线与BG的交点时,满足∠BPD是∠F的k系补周角,此时k=2n,推导见解析.
【解析】
(1)直接利用k系补周角的定义列方程求解即可.
(2)①依据k系补周角的定义及平行线的性质,建立∠BED、∠B、∠D的关系式求解即可.
②结合本题的构图特点,利用平行线的性质得到:∠ABF+∠CDF+∠F=360°,结合∠ABF=n∠ABE,∠CDF=n∠CDE(其中n为常数且n>1),又由于点P是∠ABE角平分线BG上的一个动点,通过构造相同特殊条件猜想出一个满足条件的P点,再通过推理论证得到k的值(含n的表达式),即说明点P即为所求.
解:(1)设∠H的4系补周角的度数为x,
则有120°+4x=360°,
解得:x=60°
∴∠H的4系补周角的度数为60°;
(2)①如图,

过点E作EF//AB,
∵AB//EF,
∴EF//CD,
∴∠B=∠1,∠D=∠2,
∴∠1+∠2=∠B+∠D,
即∠BED=∠B+∠D,
∵∠BED+3∠B=360°,∠D=60,
∴![]() ,
,
解得:∠B=75°,
∴∠B=75°;
②预备知识,基本构图:

如图,AB//CD//EF,则
∠ABE+∠BEG=180°,
∠DCE+∠GEC=180°,
∴∠ABE+∠BEG+∠DCE+∠GEC=360°,
即∠ABE+∠DCG+∠BEC=360°
如图:

当BG上的动点P为∠CDG的角平分线与BG的交点时,满足∠BPD是∠F的k系补周角,此时k=2n.理由如下:
若∠BPD是∠F的k系补周角,则
∠F+k∠BPD=360°,
∴k∠BPD=360°-∠F
又由基本构图知:
∠ABF+∠CDF=360°-∠F,
∴k∠BPD=∠ABF+∠CDF,
又∵∠ABF=n∠ABE,∠CDF=n∠CDE,
∴k∠BPD= n∠ABE+ n∠CDE,
∵∠BPD=∠PHD+∠PDH,
∵AB//CD,PG平分∠ABE,PD平分∠CDE,
∴∠PHD=∠ABH=![]() ,∠PDH=
,∠PDH=![]() ,
,
∴![]() (
(![]() +
+![]() )=n(∠ABE+∠CDE),
)=n(∠ABE+∠CDE),
∴k=2n.


科目:初中数学 来源: 题型:
【题目】已知:点A,B,C在同一条直线上,点M、N分别是AB、AC的中点,如果AB=10cm,AC=8cm,那么线段MN的长度为( )
A. 6cm B. 9cm C. 3cm或6cm D. 1cm或9cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,已知AB=AC,D是AC上的一点,CD=9,BC=15,BD=12.
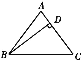
(1)证明:△BCD是直角三角形.
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校共有900名学生,学校准备调查他们对“沈阳创建卫生城”知识的了解程度,团委对部分学生采用了随机抽样调查的方式,并用收集到的数据绘制出两幅不完整的统计图(如图①、图②所示):

(1)根据图中信息,学校决定对“不了解”和“了解一点”的同学进行培训,估计该校约有多少名学生参加培训?
(2)请你直接将两个统计图补充完整.
查看答案和解析>>
科目:初中数学 来源: 题型:
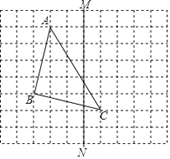
【题目】如图,在长度为1个单位的小正方形组成的正方形网格中,点A、B、C在小正方形的顶点上.
(1)在图中画出与△ABC关于直线MN成轴对称的△A1B1C1;(不写画法)
(2)请你判断△ABC的形状,并求出AC边上的高.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,∠BAC=54°,∠BAC的平分线与AB的垂直平分线OD交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC度数为( ).

A. 108° B. 135° C. 144° D. 160°
查看答案和解析>>
科目:初中数学 来源: 题型:
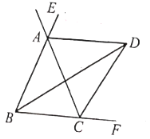
【题目】如图,![]() ,
,![]() ,
,![]() ,
,![]() 分别平分
分别平分![]() 的外角
的外角![]() ,内角
,内角![]() ,外角
,外角![]() .以下结论:①
.以下结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 平分
平分![]() ;⑤
;⑤![]() .其中正确的结论有______________.(把正确结论序号填写在横线上)
.其中正确的结论有______________.(把正确结论序号填写在横线上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角三角形纸片的两直角边长分别为6、8,按如图那样折叠,使点A与点B重合,折痕为DE,则S△BCE:S△BDE等于( )

A.2:5 B.14:25 C.16:25 D.4:21
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠A=∠B=50°,P 为 AB 中点,点 M 为射线 AC 上(不与点 A 重合)的任意一点,连接 MP, 并使MP 的延长线交射线BD 于点N,设∠BPN=α.

(1)求证:△APM≌△BPN;
(2)当 MN=2BN 时,求α的度数;
(3)若△BPN 为锐角三角形时,直接写出α的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com