
【题目】
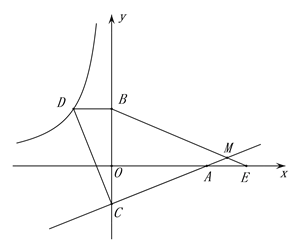
如图,已知点D在反比例函数y=![]() 的图象上,过点D作x轴的平行线交y轴于点B(0,3).过点A(5,0)的直线y=kx+b与y轴于点C,且BD=OC,tan∠OAC=
的图象上,过点D作x轴的平行线交y轴于点B(0,3).过点A(5,0)的直线y=kx+b与y轴于点C,且BD=OC,tan∠OAC=![]() .
.
(1)求反比例函数y=![]() 和直线y=kx+b的解析式;
和直线y=kx+b的解析式;
(2)连接CD,试判断线段AC与线段CD的关系,并说明理由;
(3)点E为x轴上点A右侧的一点,且AE=OC,连接BE交直线CA与点M,求∠BMC的度数.
【答案】(1)反比例函数的解析式为: ![]() 一次函数的解析式为:
一次函数的解析式为: ![]() ;
;
(2)![]() ,理由见解析;
,理由见解析;
(3)![]()
【解析】试题分析:(1)由点A(5,0)和tan∠OAC=![]() 可以求出OC=BD的长,一次函数的解析式就可以求出了,继而求出点D的坐标,反比例函数解析式就可以求出了;(2)根据已知条件,得出
可以求出OC=BD的长,一次函数的解析式就可以求出了,继而求出点D的坐标,反比例函数解析式就可以求出了;(2)根据已知条件,得出![]() ,根据等角的余角相等求出垂直关系;(3)连接AD,得出四边形AEBD为平行四边形,求出
,根据等角的余角相等求出垂直关系;(3)连接AD,得出四边形AEBD为平行四边形,求出![]() ,继而求出
,继而求出![]() .
.
试题解析:
(1)∵A(5,0),∴OA=5.
∵![]() ∴
∴![]()
∴![]()
∵![]() ∴
∴![]()
∴![]() ∴
∴![]()
设直线AC关系式为![]() ∵过A(5,0),
∵过A(5,0),![]()
∴![]() 解得:
解得: 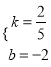 ∴
∴![]() .
.
(2)∵![]() ∴
∴![]()
∵![]() ,
,
∴![]() ,
,
∴![]() ∴
∴,
∴![]()
∴![]() .
.
(3) ![]()
连接AD,
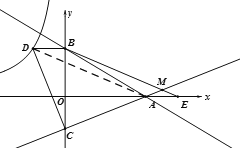
∵![]() ,
, ![]() ∴
∴![]()
∴四边形AEBD为平行四边形,∴![]() ∴
∴![]()
∵![]() ,∴
,∴![]()
∵![]() ∴
∴![]()
∴![]() =45°
=45°


科目:初中数学 来源: 题型:
【题目】多项式ax2﹣4ax﹣12a因式分解正确的是( )
A. a(x﹣6)(x+2) B. a(x﹣3)(x+4) C. a(x2﹣4x﹣12) D. a(x+6)(x﹣2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知△ABC和△EFC都是等边三角形,点E在线段AB上. 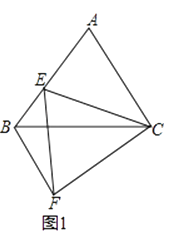
(1)求证:AE=BF,BF∥AC;
(2)若点D在直线AC上,且ED=EC(如图2),求证:AB=AD+BF; 
(3)在(2)的条件下,若点E改为在线段AB的延长线上,其它条件不变(如图3),请直接写出AB、AD、BF之间的数量关系. 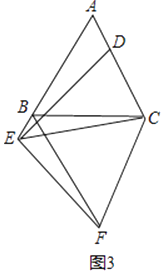
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小宇家新买的一套住房的建筑平面图如图所示(单位:米). 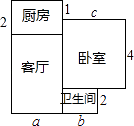
(1)这套住房的建筑总面积是多少平方米?(用含a,b,c的式子表示)
(2)若a=8,b=3,c=6,试求出小宇家这套住房的具体面积.
(3)这套住房的售价为每平方米4500元,购房时首付款为房价的40%,余款向银行申请贷款,在(2)的条件下,小宇家购买这套住房时向银行申请贷款的金额是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知三条不同的直线a,b,c在同一平面内,下列四个命题: ①如果a∥b,a⊥c,那么b⊥c;②如果b∥a,c∥a,那么b∥c;
③如果b⊥a,c⊥a,那么b⊥c; ④如果b⊥a,c⊥a,那么b∥c.
其中正确的是 . (填写序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.若两个数互为相反数,则它们的商为﹣1
B.一个数的绝对值一定不小于这个数
C.若两个数互为相反数,则这两个数一定是一个正数,一个负数
D.一个正数一定大于它的倒数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】耐心算一算(同学们,请你注意解题格式,一定要写出解题步骤哦!
(1)﹣20+(﹣14)﹣(﹣18)﹣13
(2)![]()
(3)﹣24﹣ ![]() ×[5﹣(﹣3)2].
×[5﹣(﹣3)2].
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com