
设关于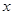 的方程
的方程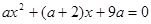 ,有两个不相等的实数根
,有两个不相等的实数根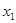 、
、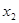 ,且
,且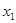
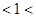
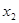 ,那么实数
,那么实数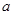 的取值范围是 ( )
的取值范围是 ( )
A.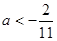 | B.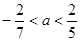 | C.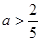 | D.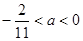 |
D
解析考点:根与系数的关系;根的判别式.
专题:转化思想.
分析:根据一元二次方程的根的判别式,建立关于a的不等式,求出a的取值范围.又存在x1<1<x2,即(x1-1)(x2-1)<0,
x1x2-(x1+x2)+1<0,利用根与系数的关系,从而最后确定a的取值范围.
解答:解:∵方程有两个不相等的实数根,
则△>0,
∴(a+2)2-4a×9a=-35a2+4a+4>0,
解得- <a<
<a<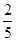 ,
,
∵x1+x2=-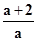 ,x1x2=9,
,x1x2=9,
又∵x1<1<x2,
∴x1-1<0,x2-1>0,
那么(x1-1)(x2-1)<0,
∴x1x2-(x1+x2)+1<0,
即9+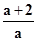 +1<0,
+1<0,
解得-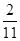 <a<0,
<a<0,
最后a的取值范围为:-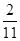 <a<0.
<a<0.
故选D.
点评:总结:1、一元二次方程根的情况与判别式△的关系:
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.
2、根与系数的关系为:x1+x2="-" 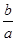 ,x1x2=
,x1x2= 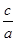
.


科目:初中数学 来源:2010年湖北省某市新人教版中考数学模拟试卷(6)(解析版) 题型:解答题
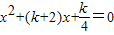 有两个不相等的实数根.
有两个不相等的实数根.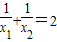 成立?若存在,请求出k的值;若不存在,请说明理由.
成立?若存在,请求出k的值;若不存在,请说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com