
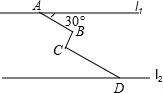
 2016年清明小长假,所有高速公路对七座以下的机动车辆免收高速费,很多人都走出家门,投入大自然的环抱,进行自驾游.如图所示,在同一平面内,两条平行高速公路l1和l2间有一条“Z”型道路连通,其中AB段与高速公路l1成30°角,长为20km;BC段与AB、CD段都垂直,长为10km,CD段长为30km,求两高速公路间的距离(结果保留根号)
2016年清明小长假,所有高速公路对七座以下的机动车辆免收高速费,很多人都走出家门,投入大自然的环抱,进行自驾游.如图所示,在同一平面内,两条平行高速公路l1和l2间有一条“Z”型道路连通,其中AB段与高速公路l1成30°角,长为20km;BC段与AB、CD段都垂直,长为10km,CD段长为30km,求两高速公路间的距离(结果保留根号) 分析 过B点作BE⊥l1,交l1于E,CD于F,l2于G.在Rt△ABE中,根据三角函数求得BE,在Rt△BCF中,根据三角函数求得BF,在Rt△DFG中,根据三角函数求得FG,再根据EG=BE+BF+FG即可求解.
解答 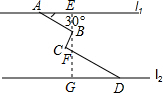 解:过B点作BE⊥l1,交l1于E,CD于F,l2于G.
解:过B点作BE⊥l1,交l1于E,CD于F,l2于G.
在Rt△ABE中,BE=AB•sin30°=20×$\frac{1}{2}$=10km,
在Rt△BCF中,BF=BC÷cos30°=10÷$\frac{\sqrt{3}}{2}$=$\frac{20\sqrt{3}}{3}$km,
CF=BF•sin30°=$\frac{20\sqrt{3}}{3}$×$\frac{1}{2}$=$\frac{10\sqrt{3}}{3}$km,
DF=CD-CF=(30-$\frac{10\sqrt{3}}{3}$)km,
在Rt△DFG中,FG=DF•sin30°=(30-$\frac{10\sqrt{3}}{3}$)×$\frac{1}{2}$=(15-$\frac{5\sqrt{3}}{3}$)km,
∴EG=BE+BF+FG=(25+5$\sqrt{3}$)km.
故两高速公路间的距离为(25+5$\sqrt{3}$)km.
点评 此题考查了解直角三角形的应用,主要是三角函数的基本概念及运算,关键把实际问题转化为数学问题加以计算.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com