
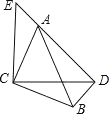
【题目】如图,△ACB和△ECD都是等腰直角三角形,△ACB的顶点A在△ECD的斜边DE上,若![]() ,则
,则![]() =___.
=___.
【答案】![]()
【解析】
根据等边三角形的性质就可以得出△AEC≌△BDC,就可以得出AE=BD,∠E=∠BDC,由等腰直角三角形的性质就可以得出∠ADB=90°,由勾股定理就可以得出:![]() ,再设AE=k,则AD=3k,BD=k,求出BC=
,再设AE=k,则AD=3k,BD=k,求出BC=![]() k,进而得到
k,进而得到
![]() 的值.
的值.
∵△ACB与△ECD都是等腰直角三角形,
∴∠ECD=∠ACB=90°,
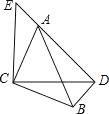
∠E=∠ADC=∠CAB=45°,EC=DC,AC=BC, ![]()
∴![]() ,∠ECD∠ACD=∠ACB∠ACD,
,∠ECD∠ACD=∠ACB∠ACD,
∴∠ACE=∠BCD.
在△AEC和△BDC中,
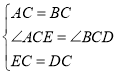 ,
,
∴△AEC≌△BDC(SAS),
∴AE=BD,∠E=∠BDC,
∴∠BDC=45°,
∴∠BDC+∠ADC=90°,
即∠ADB=90°.
∴![]() .
.
∵![]() ,
,
∴可设AE=k,则AD=3k,BD=k,
∴![]() ,
,
∴BC=![]() ,
,
∴![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题:“问有沙田一块,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知为田几何?”这道题讲的是:有一块三角形沙田,三条边长分别为5里,12里,13里,问这块沙田面积有多大?题中“里”是我国市制长度单位,1里=500米,则该沙田的面积为( )
A. 7.5平方千米 B. 15平方千米 C. 75平方千米 D. 750平方千米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,E是边CD上一点(点E不与点C、D重合),连结BE.
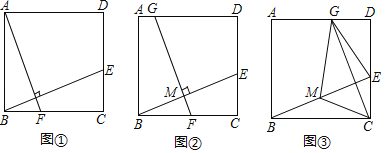
(感知)如图①,过点A作AF⊥BE交BC于点F.易证△ABF≌△BCE.(不需要证明)
(探究)如图②,取BE的中点M,过点M作FG⊥BE交BC于点F,交AD于点G.
(1)求证:BE=FG.
(2)连结CM,若CM=1,则FG的长为 .
(应用)如图③,取BE的中点M,连结CM.过点C作CG⊥BE交AD于点G,连结EG、MG.若CM=3,则四边形GMCE的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,正方形ABCD中,P是边BC上一点,BE⊥AP,DF⊥AP,垂足分别是点E、F.
(1)求证:EF=AE﹣BE;
(2)联结BF,如课![]() =
=![]() .求证:EF=EP.
.求证:EF=EP.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知用2辆A型车和1辆B型车载满货物一次可运货物10吨;用1辆A型车和2辆B型车载满货物一次可运货11吨.某物流公司现有31吨货物,计划同时租用A型车a辆,B型车b辆,一次运完,且恰好每辆车都载满货物.根据以上信息,解答下列问题:
(1)用1辆A型车和1辆B型车都载满货物一次可分别运货多少吨?
(2)请你帮该物流公司设计租车方案.若A型车每辆需租金100元/次,B型车每辆需租金120元/次.请选出最省钱的租车方案,并求出最少租车费.
查看答案和解析>>
科目:初中数学 来源: 题型:
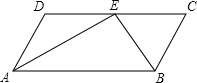
【题目】已知:如图,在四边形ABCD中,AD∥BC.点E为CD边上一点,AE与BE分别为∠DAB和∠CBA的平分线.
(1)请你添加一个适当的条件 ,使得四边形ABCD是平行四边形,并证明你的结论;
(2)作线段AB的垂直平分线交AB于点O,并以AB为直径作⊙O(要求:尺规作图,保留作图痕迹,不写作法);
(3)在(2)的条件下,⊙O交边AD于点F,连接BF,交AE于点G,若AE=4,sin∠AGF=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点![]() 若点D为BC边的中点,点M为线段EF上一动点,则
若点D为BC边的中点,点M为线段EF上一动点,则![]() 周长的最小值为
周长的最小值为![]()
![]()

A. 6 B. 8 C. 10 D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
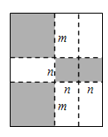
【题目】如图,将一张矩形大铁皮切割成九块,切痕如下图虚线所示,其中有两块是边长都为![]()
![]() 的大正方形,两块是边长都为
的大正方形,两块是边长都为![]()
![]() 的小正方形,五块是长宽分别是
的小正方形,五块是长宽分别是![]()
![]() 、
、![]()
![]() 的全等小矩形,且
的全等小矩形,且![]() .
.
(1)用含![]() 的代数式表示切痕的总长为
的代数式表示切痕的总长为 ![]() ;
;
(2)若每块小矩形的面积为![]() ,四个正方形的面积和为
,四个正方形的面积和为![]() ,试求该矩形大铁皮的周长.
,试求该矩形大铁皮的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如果![]() ,那么称b为n的布谷数,记为
,那么称b为n的布谷数,记为![]() .
.
例如:因为![]() ,所以
,所以![]() ,
,
因为![]() ,
,
所以![]() .
.
(1)根据布谷数的定义填空:g(2)=________________,g(32)=___________________.
(2)布谷数有如下运算性质:
若m,n为正整数,则![]() ,
,![]() .
.
根据运算性质解答下列各题:
①已知![]() ,求
,求![]() 和
和![]() 的值;
的值;
②已知![]() .求
.求![]() 和
和![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com