
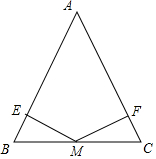
 已知AB=AC,∠BME=∠CMF,点M是BC的中点.求证:EM=FM.
已知AB=AC,∠BME=∠CMF,点M是BC的中点.求证:EM=FM.  高中必刷题系列答案
高中必刷题系列答案科目:初中数学 来源: 题型:选择题
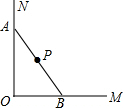 如图,一根长为a的木棍(AB),斜靠在与地面(OM)垂直的墙上,设木棍的中点为P,若木棍A端沿墙下滑,且B端沿地面向右滑动,在滑动的过程中OP的长度( )
如图,一根长为a的木棍(AB),斜靠在与地面(OM)垂直的墙上,设木棍的中点为P,若木棍A端沿墙下滑,且B端沿地面向右滑动,在滑动的过程中OP的长度( )| A. | 减小 | B. | 增大 | C. | 不变 | D. | 先减小再增大 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
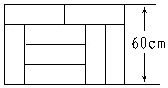 如图,8块相同的长方形地砖拼成一个长方形,每块长方形地砖的长和宽分别是x厘米和y厘米,列方程组得$\left\{\begin{array}{l}{4y=60}\\{x+y=60}\end{array}\right.$.
如图,8块相同的长方形地砖拼成一个长方形,每块长方形地砖的长和宽分别是x厘米和y厘米,列方程组得$\left\{\begin{array}{l}{4y=60}\\{x+y=60}\end{array}\right.$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 我县某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为20℃的条件下生长最快的新品种.图示是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是反比例函数y=$\frac{k}{x}$的图象上一部分.请根据图中信息解答下列问题:
我县某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为20℃的条件下生长最快的新品种.图示是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是反比例函数y=$\frac{k}{x}$的图象上一部分.请根据图中信息解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
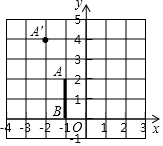 如图,在平面直角坐标系xOy中,以原点为位似中心,线段AB与线段A′B′是位似图形,若A(-1,2),B(-1,0),A′(-2,4),则B′的坐标为(-2,0).
如图,在平面直角坐标系xOy中,以原点为位似中心,线段AB与线段A′B′是位似图形,若A(-1,2),B(-1,0),A′(-2,4),则B′的坐标为(-2,0).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com