

分析 (1)根据正方形的性质和DF⊥DE,证明△DAE≌△DCF,得到DE=DF.
(2)①根据题意补全图形;
②连接HE,HF,由点H与点D关于直线EF对称,所以EH=ED,FH=FD.因为DE=DF,所以EH=FH=ED=FD.即四边形DEHF是菱形.由∠EDF=90°,得到四边形DEHF是正方形,利用正方形的性质证明△HPE≌△HCF,得到PE=CF,所以AE=PE,得到点E是AP的中点.
(3)过点F作GF⊥CF交AC的延长线于点G,利用正方形的性质证明△AEM≌△GFM,得到AM=GM,所以AG=2AM,利用勾股定理在Rt△ABC中,得到$AC=\sqrt{2}$AB,同理,在Rt△CFG中,$CG=\sqrt{2}CF$,所以$AG=AC+CG=\sqrt{2}AB+\sqrt{2}CF=\sqrt{2}(AB+CF)=\sqrt{2}(AB+AE)$,所以$2AM=\sqrt{2}(AB+AE)$,即可解答.
解答 解:(1)∵四边形ABCD是正方形,
∴DA=DC,∠DAE=∠ADC=∠DCB=90°.
∴∠DCF=180°-90°=90°.
∴∠DAE=∠DCF.
∵DF⊥DE,
∴∠EDF=90°.
∵∠ADE+∠CDE=90°,∠CDE+∠CDF=90°,
∴∠ADE=∠CDF.
在△DAE和△DCF中,
$\left\{\begin{array}{l}{∠DAE=∠DCF}\\{DA=DC}\\{∠ADE=∠CDF}\end{array}\right.$
∴△DAE≌△DCF.
∴DE=DF.
(2)①所画图形如图2所示.
②连接HE,HF,如图3.
∵点H与点D关于直线EF对称,
∴EH=ED,FH=FD.
∵DE=DF,
∴EH=FH=ED=FD.
∴四边形DEHF是菱形.
∵∠EDF=90°,
∴四边形DEHF是正方形.
∴∠DEH=∠EHF=∠HFD=90°.
∴∠AED+∠PEH=90°,∠HFC+∠DFC=90°.
∵△DAE≌△DCF,
∴∠AED=∠DFC,AE=CF.
∴∠PEH=∠HFC.
∵PH⊥CH,
∴∠PHC=90°.
∵∠PHE+∠EHC=90°,∠EHC+∠FHC=90°,
∴∠PHE=∠FHC.
在△HPE和△HCF中,
$\left\{\begin{array}{l}{∠PEH=∠HFC}\\{EH=FH}\\{∠PHE=∠FHC}\end{array}\right.$,
∴△HPE≌△HCF.
∴PE=CF.
∴AE=PE.
∴点E是AP的中点.
(3)过点F作GF⊥CF交AC的延长线于点G,如图4.
则∠GFC=90°.
∵正方形ABCD中,∠B=90°,
∴∠GFC=∠B.
∴AB∥GF.
∴∠BAC=∠G.
∵四边形ABCD是正方形,
∴AB=BC,
∴∠BAC=∠BCA=$\frac{1}{2}×$90°=45°.
∴∠BAC=∠BCA=∠FCG=∠G=45°.
∴FC=FG.
∵△DAE≌△DCF,
∴AE=CF.
∴AE=FG.
在△AEM和△GFM中,
$\left\{\begin{array}{l}{∠AME=∠GMF}\\{∠BAC=∠G}\\{AE=GF}\end{array}\right.$,
∴△AEM≌△GFM.
∴AM=GM.
∴AG=2AM,
在Rt△ABC中,$AC=\sqrt{A{B^2}+B{C^2}}=\sqrt{2A{B^2}}=\sqrt{2}AB$.
同理,在Rt△CFG中,$CG=\sqrt{2}CF$.
∴$AG=AC+CG=\sqrt{2}AB+\sqrt{2}CF=\sqrt{2}(AB+CF)=\sqrt{2}(AB+AE)$.
∴$2AM=\sqrt{2}(AB+AE)$.
∴$\frac{2AM}{AB+AE}=\sqrt{2}$.
点评 本题考查了正方形的性质,全等三角形的判定定理和性质定理,勾股定理的应用,对称的性质,解决本题的关键是利用正方形的性质得到相等的边和相等的角,证明三角形全等,作出辅助线也是解决本题的关键.


科目:初中数学 来源: 题型:解答题
 尺规作图画线段AB的垂直平分线CD(E为垂足)时,为了方便起见,通常把四段弧的半径取成相等;其实不必如此,如图,若能确保弧①、②的半径相等(即AC=BC),再确保弧③、④的半径相等(即AD=BD),直线CD同样是线段AB的垂直平分线,请你给出证明.
尺规作图画线段AB的垂直平分线CD(E为垂足)时,为了方便起见,通常把四段弧的半径取成相等;其实不必如此,如图,若能确保弧①、②的半径相等(即AC=BC),再确保弧③、④的半径相等(即AD=BD),直线CD同样是线段AB的垂直平分线,请你给出证明.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
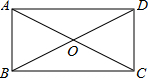 如图,矩形ABCD中,对角线AC,BD交于点O.若∠AOB=60°,BD=8,则AB的长为( )
如图,矩形ABCD中,对角线AC,BD交于点O.若∠AOB=60°,BD=8,则AB的长为( )| A. | 4 | B. | $4\sqrt{3}$ | C. | 3 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | k>-1 | B. | k<1 | C. | k>-1且k≠0 | D. | k<1且k≠0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com