练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在边长为1个单位长度的小正方形组成的网格中，点A、B、C在小正方形的顶点上.

    (1)在图中画出与△ABC关于直线l成轴对称的△A′B′C′.

    (2)四边形 ABCA′的面积为_____；

    (3)在直线l上找一点P，使PA+PB的长最短，则这个最短长度为______.

    【答案】(1)见解析；(2)；(3).

    【解析】

    （1）根据题意作出图形即可；

    （2）用割补法求解即可得到结论；

    （3）作出图形，根据勾股定理求得结果即可．

    （1）如图所示，△A'B'C'即为所求；

    （2）四边形ABCA'的面积=4×42×11×43×3=；

    （3）连接AB'交直线l与点P，

    则PA+PB长的最短值=AB'，∴AB'；∴这个最短长度为．

    故答案为：，．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】在Rt△ABC中，∠C=90°，AC=6，BC=8（如图），点D是边AB上一点，把△ABC绕着点D旋转90°得到△A'B'C'，边B'C'与边AB相交于点E，如果AD=BE，那么AD长为__．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下列材料，学习完“代人消元法”和“加减消元法“解二元一次方程组后，善于思考的小铭在解方程组时，采用了一种“整体代换”的解法：

    解：将方程②变形：4x+10y+y=5即2(2x+5y)+y=5③

    把方程①代入③得：2×3+y=5，∴y=-1①得x=4，所以，方程组的解为．

    请你解决以下问题：

    (1)模仿小铭的“整体代换”法解方程组．

    (2)已知x，y满足方程组，求x2+4y2的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校在推进新课改的过程中，开设的“课程超市”有：A．炫彩剧社，B．烹饪，C．游泳，D．羽毛球，E．科技等五个科目，学生可根据自己的爱好选修一门，负责“课程超市”的老师对七年级一班全体同学的选课情况进行调查统计，并将结果绘制成了如下两幅尚不完整的统计图：

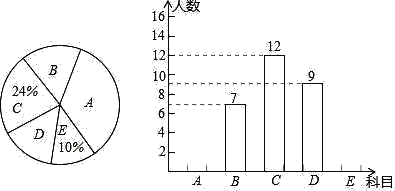
    根据图中提供的信息，解答下列问题：

    （1）请求出该班的总人数；

    （2）扇形统计图中，D所在扇形的圆心角度数为　 　，并补全条形统计图；

    （3）该班班委4人中，1人选修炫彩剧社，2人选修烹饪，1人选修游泳，老师要从这4人中任选2人了解他们对“课程超市”课程安排的看法，请你用列表或画树状图的方法，求选出的2人恰好1人选修炫彩剧社，1人选修烹饪的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】图1和图2，半圆O的直径AB=2，点P（不与点A，B重合）为半圆上一点，将图形延BP折叠，分别得到点A，O的对称点A′，O′，设∠ABP=α．

    （1）当α=15°时，过点A′作A′C∥AB，如图1，判断A′C与半圆O的位置关系，并说明理由．

    （2）如图2，当α= °时，BA′与半圆O相切．当α= °时，点O′落在上．

    （3）当线段BO′与半圆O只有一个公共点B时，求α的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为表彰在某活动中表现积极的同学，老师决定购买文具盒与钢笔作为奖品．已知5个文具盒、2支钢笔共需100元；3个文具盒、1支钢笔共需57元．

    （1）每个文具盒、每支钢笔各多少元？

    （2）若本次表彰活动，老师决定购买10件作为奖品，若购买个文具盒，10件奖品共需元，求与的函数关系式．如果至少需要购买3个文具盒，本次活动老师最多需要花多少钱？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

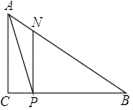
    【题目】如图在△ABC中，∠C=90°，AC=3cm，BC=4cm，点P是边BC上由B向C运动（不与点B、C重合）的一动点，P点的速度是1cm/s，设点P的运动时间为t，过P点作AC的平行线交AB与点N，连接AP，

    （1）请用含有t的代数式表示线段AN和线段PN的长，

    （2）当t为何值时，△APN的面积等于△ACP面积的三分之一？

    （3）在点P的运动过程中，是否存在某一时刻的t的值，使得△APN的面积有最大值，若存在请求出t的值并计算最大面积；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，等腰△ABC中，AB=AC=10，BC=16，点F是边BC上不与点B，C重合的一个动点，直线DE垂直平分BF，垂足为D.当△ACF是直角三角形时，线段BD的长为__________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下面材料，完成（1）-（3）题
    数学课上，老师出示了这样一道题：如图， 中，，点P为边AB上一点（不与A、B重合），过P作于Q，做QE∥AB交BC于点E，连接PE，将线段PE绕点P顺时针旋转90°到PF，连接QF，探究线段之间的数量关系并证明．
    同学们经过思考后，交流了自已的想法
    小明：“通过观察和度量，发现为直角．”
    小伟：“我通过一线三直角的模型构造三角形全等可以解决问题．”
    小强：“我构造等腰直角三角形，再利用全等三角形可以解决问题．”
    老师：“若其他条件不变，PE=AC，就可以求出的值．”
    （1）多少度？四边形为什么特殊四边形？（直接写出答案）
    （2）探究线段之间的数量关系并证明；
    （3）若其他条件不变，PE=AC，求的值．

    查看答案和解析>>

    同步练习册答案