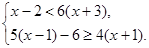分析:(1)将不等式两边同乘以2,再根据移项、合并同类项、系数化为1,求出不等式的解集;
(2)由题意知将不等式组中的不等式的解集根据移项、合并同类项、系数化为1分别解出来,然后再根据解不等式组解集的口诀:大小小大中间找,来求出不等式组的解.
(3)由题意知将不等式组中的不等式的解集根据移项、合并同类项、系数化为1分别解出来,然后再根据解不等式组解集的口诀:同大取大,来求出不等式组的解;
(4)将方程两边乘以x-2,然后再根据移项、系数化为1,求出方程的解;
(5)将方程两边乘以2x+6,然后再根据移项、系数化为1,从而求出方程的解;
(6)将方程两边乘以x-2,然后再根据移项、系数化为1,求出方程的解;
解答:解:(1)由方程
-1≤两边同乘以2得
x-5-2≤3x+2,
∴2x≥-9,
∴x≥-
;
(2)由不等式3x+2>2x-2,
移项得x>-4,
由不等式4x-3≤3x-2,
移项得x≤1,
∴不等式解集为:-4<x≤1;
(3)由不等式5x-2>3x+3移项得
2x>5,
解得x>2.5,
由不等式x-2≥14-3x移项得
4x≥16,
解得x≥4,
∴不等式解集为:x≥4;
(4)方程
=2-
两边同乘以x-2(x-2≠0)得
3=2x-4-x,
解得x=7;
(5)方程
+
=
两边同乘以2(x+3)(x+3≠0)得
4+3(x+3)=4,
解得x=-3,
∵x+3≠0,
∴x≠-3,
∴方程无解;
(6)方程
+3=
两边同乘以x-2(x-2≠0)得
1+3x-6=x-1,
解得x=2,
∵x-2≠0,
∴x≠2,
∴方程无解.
点评:(1)此问考查不等式的一般解法:移项、系数化为1等,比较简单;
(2)、(3)主要考查了一元一次不等式组解集的求法,利用不等式组解集的口诀:同大取大,同小取小,大小小大中间找,大大小小找不到(无解),来求解.
(4)(5)(6)都是考查解方程的一般方法,首先找出方程分母最大公约数,将其乘以方程的两边,再根据移项、合并同类项、系数化为1来求解,同时注意分母不为0的情况,这是容易出错的地方.



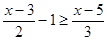 ;
; 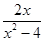 +
+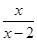 =1.
=1.