
【题目】古希腊著名的毕达哥拉斯学派把1,3,6,10…这样的数称为“三角形数”,而把1,4,9,16…这样的数称为“正方形数”.观察下面的点阵图和相应的等式,探究其中的规律:
(1)下图反映了任何一个三角形数是如何得到的,认真观察,并在④后面的横线上写出相应的等式;
![]()

(2)通过猜想,写出(1)中与第八个点阵相对应的等式 ;
(3)从下图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.结合(1)观察下列点阵图,并在⑤看面的横线上写出相应的等式.


(4)通过猜想,写出(3)中与第n个点阵相对应的等式 ;
(5)判断256是不是正方形数,如果不是,说明理由;如果是,256可以看作哪两个相邻的“三角形数”之和?
【答案】(1)1+2+3+4=![]() =10;(2)1+2+3+…+8=
=10;(2)1+2+3+…+8=![]() ;(3)10+15=52;(4)
;(3)10+15=52;(4)![]() =n2;(5)是正方形数,可以看作是120、136两个相邻的三角形数的和.
=n2;(5)是正方形数,可以看作是120、136两个相邻的三角形数的和.
【解析】
(1)根据计算方法写出即可;
(2)根据求解规律,用点阵的序数乘比序数大1的数,再除以2即可;
(3)根据(1)中三角形数的规律写出即可;
(4)用第(n1)个三角形数加上第n个三角形数,整理即可得解;
(5)根据256=162可得是正方形数,然后再计算三角形数即可.
解:(1)④1+2+3+4=![]() =10;
=10;
(2)第八个点阵相应的等式:1+2+3+…+8=![]() ;
;
(3)⑤10+15=52;
(4)第n个点阵相对应的等式:![]() =n2;
=n2;
(5)∵256=162,
∴256是正方形数,
而1+2+3+…+16=136,1+2+3+…+15=120,
∴可以看作是120、136这两个相邻的三角形数的和.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】小明和小刚相约周末到雪莲大剧院看演出,他们的家分别距离剧院1200m和2000m,两人分别从家中同时出发,已知小明和小刚的速度比是3:4,结果小明比小刚提前4min到达剧院.求两人的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以正方形![]() 的顶点
的顶点![]() 为坐标原点,直线
为坐标原点,直线![]() 为
为![]() 轴建立直角坐标系,对角线
轴建立直角坐标系,对角线![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() 为
为![]() 上一点,点
上一点,点![]() 坐标为
坐标为![]() ,则点
,则点![]() 绕点
绕点![]() 顺时针旋转90°得到的对应点
顺时针旋转90°得到的对应点![]() 的坐标是( )
的坐标是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装公司招工广告承诺:熟练工人每月工资至少4000元.每天工作8小时,一个月工作25天.月工资底薪1000元,另加计件工资.加工1件A型服装计酬20元,加工1件B型服装计酬15元.在工作中发现一名熟练工加工2件A型服装和3件B型服装需7小时,加工1件A型服装和2件B型服装需4小时.(工人月工资=底薪+计件工资)
(1)一名熟练工加工1件A型服装和1件B型服装各需要多少小时?
(2)一段时间后,公司规定:“每名工人每月必须加工A,B两种型号的服装,且加工A型服装数量不少于B型服装的一半”.设一名熟练工人每月加工A型服装a件,工资总额为W元.请你运用所学知识判断该公司在执行规定后是否违背了广告承诺?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 三边长分别为
三边长分别为![]() 、
、![]() 、
、![]() ,求这个三角形的面积,小明同学在求面积时先画了一个每个小正方形的边长均为1的正方形网格,再在网格中画出格点
,求这个三角形的面积,小明同学在求面积时先画了一个每个小正方形的边长均为1的正方形网格,再在网格中画出格点![]() (
(![]() 各个顶点都在网格的格点上).如图1所示,这样借用网格(不需
各个顶点都在网格的格点上).如图1所示,这样借用网格(不需![]() 的高)就能算出三角形的面积,这种方法叫构造法.
的高)就能算出三角形的面积,这种方法叫构造法.
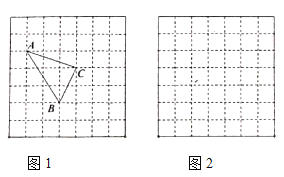
(1)![]() 的面积为___________________.
的面积为___________________.
(2)若![]() 的三边长分别为
的三边长分别为![]() 、
、![]() 、
、![]() ,请在图2的网格中画出
,请在图2的网格中画出![]() ,使得
,使得![]() 的三个顶点都在格点上,求此三角形的面积.
的三个顶点都在格点上,求此三角形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B在直线1上,AB = 20cm,∠BAC= 120°.

(1)点P从A出发,沿射线AB以每秒2cm的速度向右运动,同时点Q从B出发,沿射线BA以每秒lcm的速度向左运动,求点P出发多少秒时与点Q重合?
(2)在(1)的条件下,求点P出发多少秒时与点Q相距5cm?
(3)点M为射线AC上一点,AM = 4cm,现将射线AC绕点A以每秒30°的速度顺时针旋转一周后停止,同时点N从点B出发沿直线AB向左运动,在这一运动过程中,是否存在某一时刻,使得点N为BM的中点?若存在,求出点N运动的速度:若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下面的情景,回答问题:
小王逛超市看到如下两个超市的促销信息

备注:假设两家超市相同的标价都一样.
(1)当一次性购买标价总额是400元时,甲、乙超市实际付款分别是多少?
(2)当标价总额是多少时,甲、乙超市实付款一样?
(3)小王两次到乙超市分别购物付款189元和474元,若他只去一次该超市购买同样多的商品,可以节省多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,请在下列四个关系中,选出两个恰当的关系作为条件,推出四边形ABCD是平行四边形,并予以证明.(写出一种即可)
关系:①AD∥BC,②AB=CD,③∠A=∠C,④∠B+∠C=180°.
已知:在四边形ABCD中, , ;
求证:四边形ABCD是平行四边形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com