
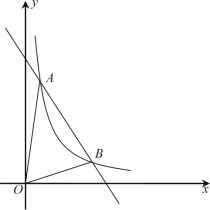
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于A(m,6),B(3,n)两点.
的图象交于A(m,6),B(3,n)两点.
(1)求一次函数的解析式;
(2)求![]() 的面积;
的面积;
(3)根据图象直接写出![]() 的x的取值范围
的x的取值范围
 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 经过
经过![]() ,
,![]() 两点,且与
两点,且与![]() 轴交于点
轴交于点![]() ,抛物线的对称轴是直线
,抛物线的对称轴是直线![]() .
.
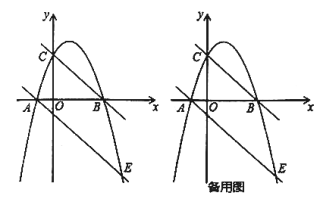
(1)求抛物线的函数表达式;
(2)抛物线与直线![]() 交于
交于![]() 、
、![]() 两点,
两点,![]() 点在
点在![]() 轴上且位于点
轴上且位于点![]() 的左侧,若以
的左侧,若以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似,求点
相似,求点![]() 的坐标;
的坐标;
(3)![]() 是直线
是直线![]() 上一动点,
上一动点,![]() 为抛物线上一动点,若
为抛物线上一动点,若![]() 为等腰直角三角形,请直接写出点
为等腰直角三角形,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
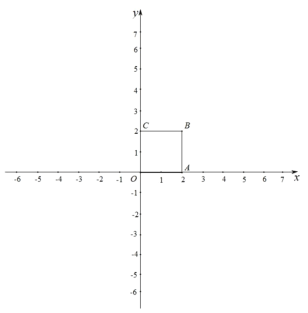
【题目】对于平面内的点 P 和图形 M,给出如下定义:以点 P 为圆心,以 r 为半径作⊙P,使得图形 M 上的所有点都在⊙P 的内部(或边上),当 r 最小时,称⊙P 为图形 M 的 P 点 控制圆,此时,⊙P 的半径称为图形 M 的 P 点控制半径.已知,在平面直角坐标系中, 正方形 OABC 的位置如图所示,其中点 B(2,2)
(1)已知点 D(1,0),正方形 OABC 的 D 点控制半径为 r1,正方形 OABC 的 A 点 控制半径为 r2,请比较大小:r1 r2;
(2)连接 OB,点 F 是线段 OB 上的点,直线 l:y= ![]() x+b;若存在正方形 OABC 的 F点控制圆与直线 l 有两个交点,求 b 的取值范围.
x+b;若存在正方形 OABC 的 F点控制圆与直线 l 有两个交点,求 b 的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
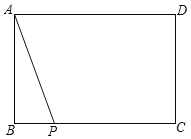
【题目】如图,已知矩形ABCD中,AB=3,BC=5,P是线段BC上的一动点.
(1)请用不带刻度的直尺和圆规,按下列要求作图:(不要求写作法,但保留作图痕迹),在CD边上确定一点E,使得∠DEP+∠APB=180°;
(2)在(1)的条件下,点P从点B移动到点C的过程中,对应点E随之运动,则移动过程中点E经过的总路程长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,对角线AC为⊙O的直径,过点C作AC的垂线交AD的延长线于点E,点F为CE的中点,连接DB,DC,DF.

(1)求∠CDE的度数;
(2)求证:DF是⊙O的切线;
(3)若AC=2![]() DE,求tan∠ABD的值.
DE,求tan∠ABD的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】草莓是云南多地盛产的一种水果,今年某水果销售店在草莓销售旺季试销售成本为每千克18元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克40元.经试销发现,销售量y(kg)与销售单价x(元/kg)符合一次函数关系,如图是y与x的函数关系图象.
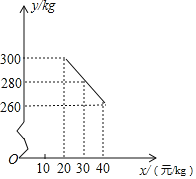
(1)求y与x的函数解析式;
(2)设该水果销售店试销草莓获得的利润为W元,求W的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形![]() 中,
中,![]() 是边
是边![]() 上的一动点(不与点
上的一动点(不与点![]() 、
、![]() 重合),连接
重合),连接![]() ,点
,点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() .
.
(1)求证:![]() ;
;
(2)用等式表示线段![]() 与
与![]() 的数量关系,并证明.
的数量关系,并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2+2x﹣3与x轴交于A,B两点(点A在点B的左侧),将这条抛物线向右平移m(m>0)个单位长度,平移后的抛物线与x轴交于C,D两点(点C在点D的左侧),若B,C是线段AD的三等分点,则m的值为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子中装有大小和形状相同的3个红球和2个白球,把它们充分搅匀.
(1)“从中任意抽取1个球不是红球就是白球”是 事件,“从中任意抽取1个球是黑球”是 事件;
(2)从中任意抽取1个球恰好是红球的概率是 ;
(3)学校决定在甲、乙两名同学中选取一名作为学生代表发言,制定如下规则:从盒子中任取两个球,若两球同色,则选甲;若两球异色,则选乙.你认为这个规则公平吗?请用列表法或画树状图法加以说明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com