
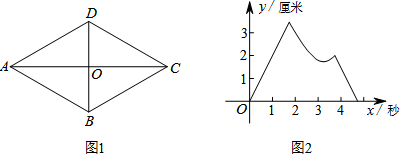
| A. | 点P:O-A-D-C,点Q:O-C-D-O | B. | 点P:O-A-D-O,点Q:O-C-B-O | ||
| C. | 点P:O-A-B-C,点Q:O-C-D-O | D. | 点P:O-A-D-O,点Q:O-C-D-O |
分析 先根据图1中不同路线的位置,判断P,Q间的距离的变换情况,再结合图2中函数图象的变换趋势进行判断分析.
解答 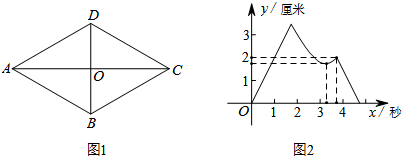 解:∵菱形ABCD中,AB=2,∠BAD=60°
解:∵菱形ABCD中,AB=2,∠BAD=60°
∴AO=CO=$\sqrt{3}$,DO=BO=1
(A)若点P:O-A-D-C,点Q:O-C-D-O,则当x=2+$\sqrt{3}$时,y=0,与图2不符,故(A)错误;
(B)若点P:O-A-D-O,点Q:O-C-B-O,则当x=2$\sqrt{3}$时,y有最大值,当x=$\frac{3}{2}$+$\sqrt{3}$时,y=$\sqrt{3}$,当x=3+$\sqrt{3}$时,y=0,与图2相符,故(B)正确;
(C)当点P与点Q运动完时,点P在点C上,点Q在点O上,所以y=$\sqrt{3}$,与图2不符,故(C)错误;
(D)若点P:O-A-D-O,点Q:O-C-D-O,则当x=2+$\sqrt{3}$时,y=0,与图2不符,故(D)错误.
故选(B)
点评 本题主要考查了动点问题的函数图象以及菱形的性质,用图象分析问题时,要理清图象的含义,即会识图.函数图象是典型的数形结合,通过看图获取图象中关键点所包含的信息,是解决问题的关键.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 加,加 | B. | 加,减 | C. | 减,加 | D. | 减,减 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{20x+60y=280}\\{x-y=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{60x+20y=280}\\{x-y=2}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{20x+60y=280}\\{y-x=2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{60x+20y=280}\\{y-x=2}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
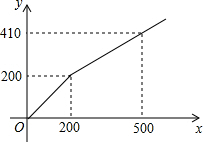 某商店在节日期间开展优惠促销活动:购买原价超过200元的商品,超过200元的部分可以享受打折优惠.若购买商品的实际付款金额y(单位:元)与商品原价x(单位:元)的函数关系的图象如图所示,则超过200元的部分可以享受的优惠是( )
某商店在节日期间开展优惠促销活动:购买原价超过200元的商品,超过200元的部分可以享受打折优惠.若购买商品的实际付款金额y(单位:元)与商品原价x(单位:元)的函数关系的图象如图所示,则超过200元的部分可以享受的优惠是( )| A. | 打八折 | B. | 打七折 | C. | 打六折 | D. | 打五折 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 10 | B. | 15 | C. | 13 | D. | 14 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
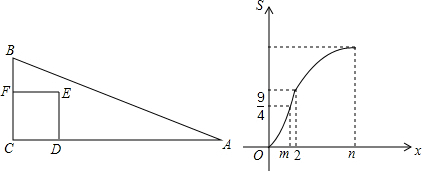
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com